1. KIẾN THỨC CƠ BẢN 1. Góc giữa hai mặt phẳng

Định nghĩa

Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phăng đó.

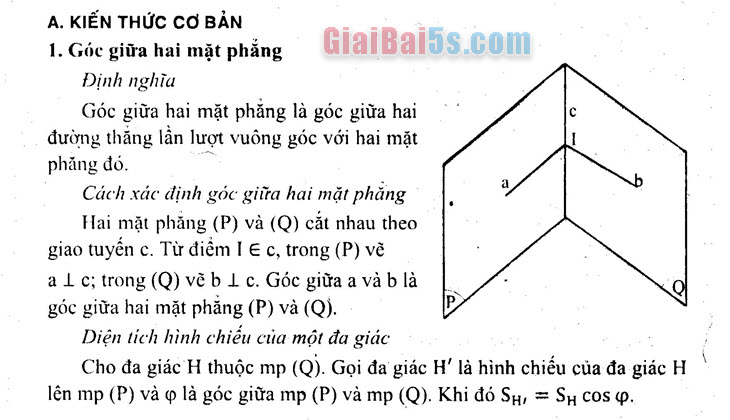
Cách xác định góc giữa hai mặt phẳng

Hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Từ điểm IE c, trong (P) về a 1 c; trong (Q) vẽ b l c. Góc giữa a và b là góc giữa hai mặt phẳng (P) và (Q).

Diện tích hình chiếu của một đa giác

Cho đa giác H thuộc mp (Q). Gọi đa giác H’ là hình chiếu của đa giác H lên mp (P) và ý là góc giữa mp (P) và mp (Q). Khi đó SH = SH cos p.

2. Hai mặt phẳng vuông góc . Định nghĩa

Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là góc vuông. | Định lí và hệ quả – Định lí 1 (điều kiện để hai mặt phẳng vuông góc)

Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Ja C (P) = (P)1(Q).

la1(Q) | – Hệ quả 1

Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau thì bất cứ đường thẳng a nào nằm trong (P), vuông góc với giao tuyến của (P) và (Q) thì đều vuông góc với (Q).

(d = (P) n(Q);(P) 1 (0) ac (P)

al (Q). laid – Hệ qua 2

Nếu hai mặt phẳng (P) và (Q) vuông góc { với nhau và A là một điểm nằm trong (P) thì

đường thẳng đi qua điểm A và vuông góc với (Q) sẽ nằm trong (P).

((P) 1(Q) JAE (P) Jal(l) \A Ea – Định lí 2 .

Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

(a = (P) n(Q) {(P) 1 (R) a I (R). .. ((0) 1 (R)

mať (P).

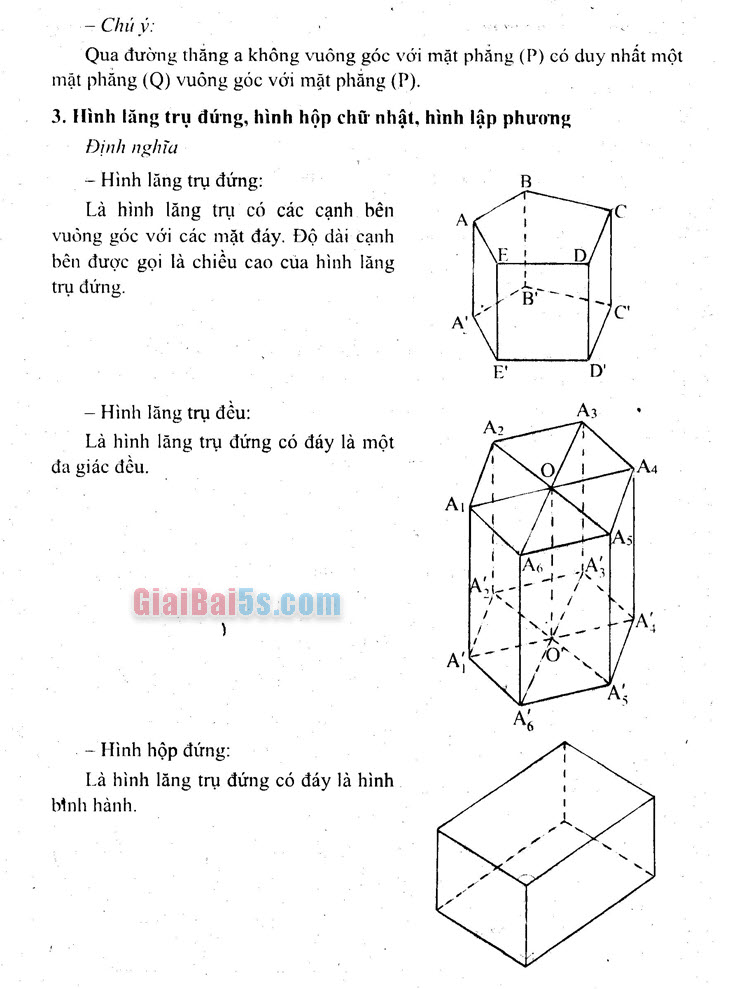
– Chú ý: ỖQua đường thẳng a không vuông góc với mặt phẳng (P) có duy nhất một mặt phẳng (Q) vuông góc với mặt phẳng (P). 3. Hình lăng trụ đúng, hình hộp chữ nhật, hình lập phương | Định nghĩa – Hình lăng trụ đứng:

LB : Là hình lăng trụ có các cạnh bên vuông góc với các mặt đáy. Độ dài cạnh | bên được gọi là chiều cao của hình lăng trụ đứng.

А

!

Ei

L-

BR

|

– Hình lăng trụ đều:

Là hình lăng trụ đứng có đáy là một đa giác đều.

AIRL

Arne

– Hình hộp đứng:

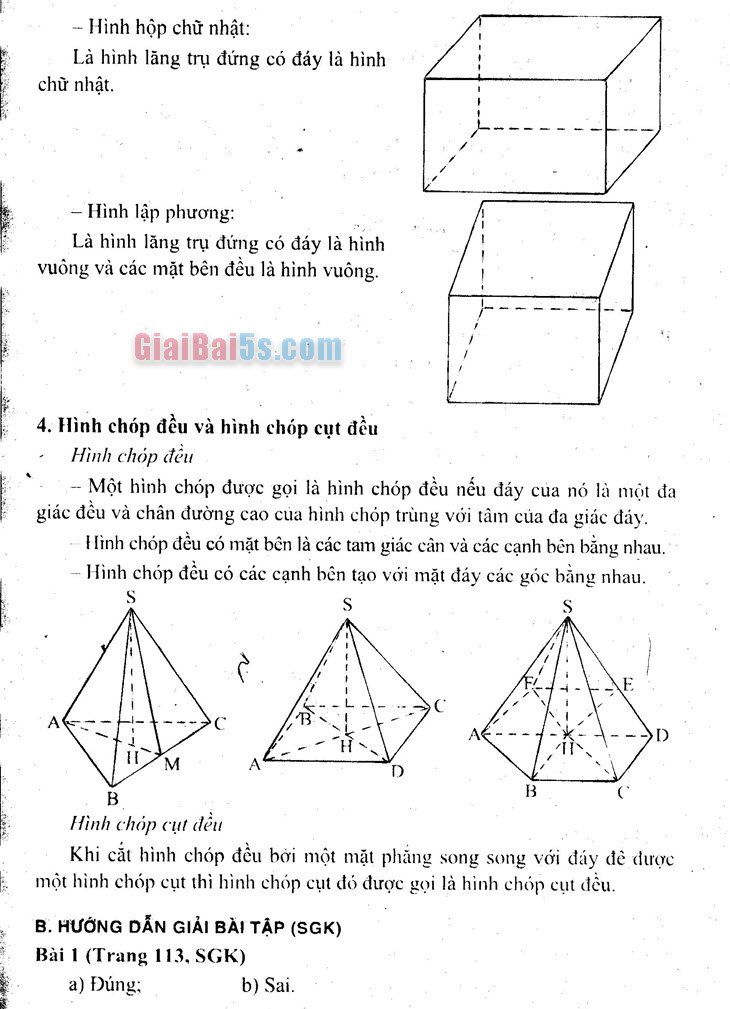
– Hình hộp chữ nhật:

Là hình lăng trụ đứng có đáy là hình | chữ nhật.

– Hình lập phương:

Là hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông.

|

4. Hình chóp đều và hình chóp cụt đều

Hình chóp đều

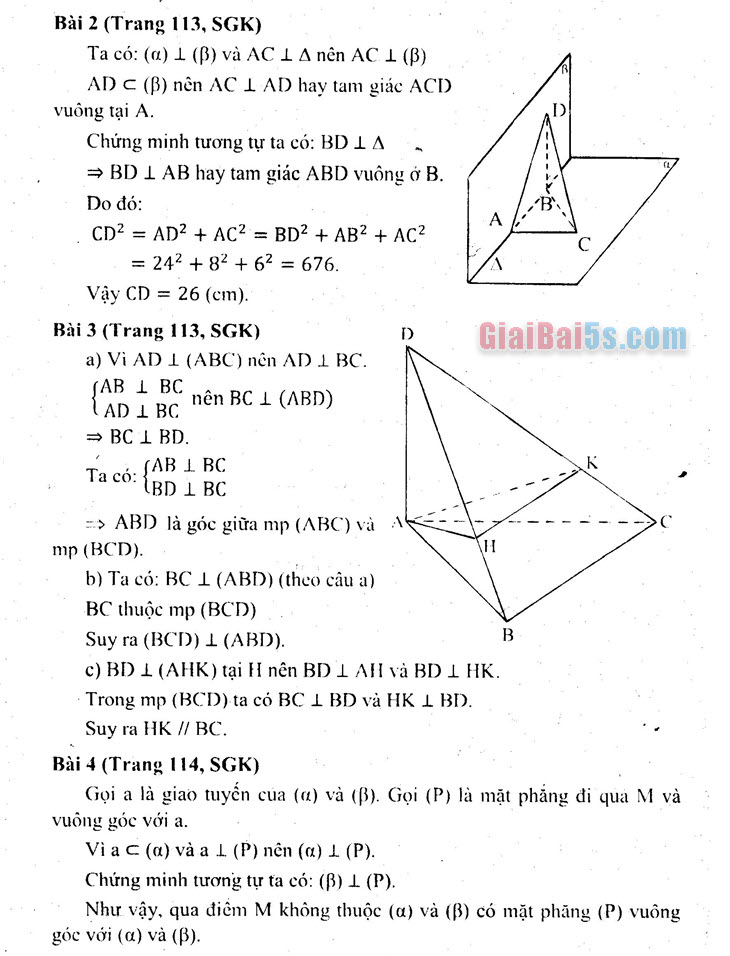
– Một hình chóp được gọi là hình chóp đều nếu đáy của nó là một đa giác đều và chân đường cao của hình chóp trùng với tâm của đa giác đáy.

– Tình chóp đều có mặt bên là các tam giác cân và các cạnh bên bằng nhau. – Hình chóp đều có các cạnh bên tạo với mặt đáy các góc bằng nhau.

M

–

–

–

–

–

–

–

/

*

—

|

. B Hình chóp cụt đều

Khi cắt hình chóp đều bởi một mặt phẳng song song với đáy để được một hình chóp cụt thì hình chóp cụt đó được gọi là hình chóp cụt đểu. B. HƯỚNG DẪN GIẢI BÀI TẬP (SGK) Bài 1 (Trang 113, SGK)

1. a) Đúng, . b) Sai. .

Bài 2 (Trang 113, SGK)

Ta có: (a) 1 (8) và ACIA nên AC 1 (8)

AD C (B) nên AC 1 AD hay tam giác ACD vuông tại A.

Chứng minh tương tự ta có: BD 1A , = BD 1 AB hay tam giác ABD vuông ở B. Do đó: CD2 = ADP + AC? = BD2 + AB? + AC?

= 242 + 82 +62 = 676. Vậy CD = 26 (cm). Bài 3 (Trang 113, SGK)

1. a) Vì AD 1 (ABC) nên AD 1 BC.

LA

(AB 1 BC nên BC 1 (ABD)

CAD IBC = BC I BD.

Ta có: AB 1 BỘ

–

—

—

—

‘IBD i BC -> ABD là góc giữa mp (ABC) và AK— mp (BCD).

1. b) Ta có: BC (ABD) (theo câu a) . BC thuộc mp (BCD). Suy ra (BCD) (ABID). c) BD 1 (AHK) tại II nên BDI AI và BD I HK. Trong mp (BCD) ta có BC 1 BD và HK 1 BD.

Suy ra HK // BC. Bài 4 (Trang 114, SGK)

Gọi a là giao tuyến của (1) và (3). Gọi (P) là mặt phẳng đi qua M và vuông góc với a.

Vì a c (a) và a I (P) nên (1) + (P). Chứng minh tương tự ta có: (8) 1 (P).

Như vậy, qua điểm M không thuộc (3) và (B) có mặt phẳng (P) vuông góc với (a) và (3).

.

Như vậy, 9

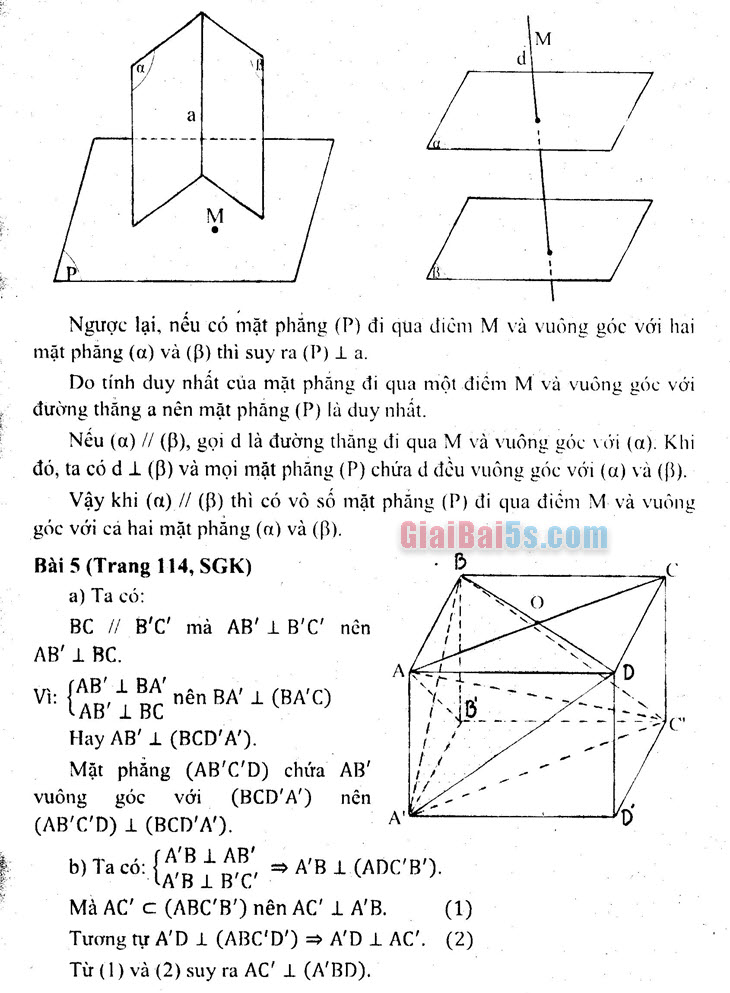
Ngược lại, nếu có mặt phẳng (P) đi qua điềui M và vuông góc với hai mặt phẳng (d) và (8) thì suy ra (P) I a.

ỖDo tính duy nhất của mặt phẳng đi qua một điểm M và vuông góc với đường thẳng a nên mặt phẳng (P) là duy nhất.

Nếu (a) // (8), gọi d là đường thẳng đi qua M và vuông góc với (a). Khi đó, ta có d1 (B) và mọi mặt phẳng (P) chứa d đều vuông góc với (a) và (3). | Vậy khi (1) // (8) thì có vô số mặt phẳng (P) đi qua điểm M và vuông góc với cả hai mặt phẳng (a) và (8). Bài 5 (Trang 114, SGK)

1. a) Ta có:

BC | B’C’ mà AB’ 1 B’C’ nên , AB’ 1 BC. Vi. SAB’ I BA’

– nên BA’ I (BA’C) . “LAB’ 1 BC”

Hay AB’ I (BCD’A’).

Mặt phẳng (AB’C’D) chứa AB : vuông góc với (BCD’A’) nên • (AB’C’D) I (BCD’A’). b) Ta có: {.

SA’B I AB’ A’B I(ADC’B’). a. LABI B’C’ ADLI Mà AC c (ABC’B’) nên AC’ 1 AB. (1) Tương tự AD 1 (ABC’D’) = AD 1 AC’. (2) Từ (1) và (2) suy ra AC’ 1 (A’BD).

AK

: AVEC

Vi SAC I BD

Bài 6 (Trang 114, SGK)

1. a) Gọi O là tâm của hình thoi ABCD. Do đó, 0 là trung điểm của AC và BD, AC và BD là hai đường chéo của hình thoi ABCD nên AC 1 CD. Tam giác SAC có SA = SC nên cân tại S. SO là trung tuyến nên đồng thời cũng là đường cao ứng với AC. Suy ra SO I AC. VIAC I Son

nên AC 1 (SBD). Mà AC C (ABCD). Suy ra (ABCD)1 (SBD).

1. b) Theo giá thiết ta có: SA = SB = a ! SC = AB = BC = a. | = ASAC, ABAC và ADAC là các tam giác cân và bằng nhau.

Do đó os = OB = OD (cùng là đường trung tuyến ứng với cạnh AC). Ta – có: S() = BD. Vậy ASBD là tam giác vuông tại S.

| Bài 7 (Trang 114, SGK)

1. a) Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên ta có: ŞAD I AB = AD I (ABB’A’). LAD I AA > AD I (ABB’A’). .

Mà AD C. (ADC’B’).” = (ADC’B’) 1 (ABB’A’).

B’ b) Tam giác Acc’ vuông tại C. Áp dụng định lí Pi-ta-go ta có: AC2 = AC2 + CC’? Tam giác ABC vuông tại B

: D . nên ta có: AC2 = AB2 + BC2

Suy ra AC’2 = AB2 + BC2 + CC’2 = a 2 + b2 + c?.

Vậy AC = Va? + b2 + c^. Bài 8 (Trang 114, SGK) | Vận dụng kết quả câu b) bài 7.

Với trường hợp a = b = c ta có độ dài đường chéo hình lập phương là a/3.

ATI

Bài 9 (Trang 114, SGK) | SH là đường cao của hình chóp đều S.ABC nên H là tâm của tam giác đều ABC.

Suy ra AH 1 BC. SH (ABC) nên SH 1 BC. ..

n AH 1 BC nên BC 1 (SAH). WISH I BC > BC I SA. Tương tự:

AC 1 BH nên AC l (SHB). LAC I SH” > AC I SB.

B Bài 10 (Trang 114, SGK) | a) 0 là tâm của hình vuông đáy ABCD của hình chóp tứ giác đều S.ABCD. | Do đó SO I (ABCD).

= ASOA vuông tại O.

ABCD là hình vuông cạnh a Bé . nên độ dài đường chéo AC là a/2. Suy ra OA = OC = a12

ARAS

ra

AS

Xét tam giác vuông SOA, áp. dụng định lí Pi-ta-go, ta có:

SA? = $02 + 0A? => SO’=SA – OA’=a?- (172)

(1)

Suy ra S0 = av? b) ASBC là tam giác đều cạnh a nên BM 1 SC. ASDC là tam giác đều cạnh a nên DM 1 SC. Từ (1) và (2) suy ra SC I (MBD). | Mà SCC (SAC) nên (SAC) 1 (MBD).

. (2)

1. c) OM là đường trung tuyến của tam giác cân SOC nên OM cũng là đường cao ứng với cạnh SC.

Suy ra OM 1 SC hay AOMC vuông tại M. . . Áp dụng định lí Pi-ta-go, ta có:

OM’+MC’ =0C OM’ = OC? – MC =

2

4

4

Do đó: OM =.

SC

a

M là trung điểm của SC nên MC = = = AOMC vuông cân tại M. Do đó MỘC = 450. BD là giao tuyến giữa hai mặt phẳng (MBD) và (ABCD).

M0 1 BD và CO 1 BD suy ra góc Mọc là góc giữa hai mặt phẳng • (MBD) và (ABCD).

| Vậy góc giữa hai mặt phẳng (MBD) và (ABCD) là góc M0C và bằng 45°. Bài 11 (Trang 114, SGK)

1. a) Ta có: ABCD là hình thoi nên hai đường chéo AC và BD vuông góc. SC 1 (ABCD), BD c (ABCD) nền SC 1 BD.

BDI SC IBD LAC

= BD 1 (SAC). | Mà BD c (SBD) nến (SBD) 1 (SAC).

by ABCD là hình thoi nên AB = BC = CD = DA = a

Góc A = 60o nên AABD, ABCD là hai tam giác đều.

1. SC I (ABCD) nên tam giác SCA vuông tại S. Hai tam giác vuông AIKA và ASCA đồng dạng (g.g)

IK AL SC SA

DAKI

Xét tam giác vuông SCA, theo định lí Pi-ta-go ta có:

? 18a

$A°=scotac* – * (105) – 187 => SA – BAR

|

SA

SA

3a

ñ

aV6 av3 Thay giá trị của SA vào (*) ta có: JK – SC.

: 12 c) ABCD là tam giác đều, I là trung điểm BD nên có: IB = ID= BD = = IK = 1B = ID ; Xét ABCD, có IK là trung tuyến ứng với cạnh BD và IK = IB = ID. Suy ra ABKD là tam giác vuông tại K. Do đó BK) – 90.

nên SA l (BKD) SA 1 BK và SA 1 DK. TSAIIK Mà SA là giao tuyến của hai mặt phẳng (SAB) và (SAD). Suy ra BKD là góc giữa hai mặt phẳng (SAB) và (SAD) và góc đó

Vi {SA IBD

|

bằng 90