1. KIẾN THỨC CƠ BẢN 1. Khoảng cách từ một điểm đến một mặt phẳng, đến một đường thẳng

Định nghĩa 1

Khoảng cách từ một điểm M đến mặt phẳng (P) (hoặc đến đường thẳng A) là khoảng cách giữa điểm M và II, trong đó II là hình chiếu của điểm M trên mặt phẳng (P), kí hiệu là dễM, (P)) (hoặc trên đường thẳng A, kí hiệu là . d(M,4))..

2. Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai | mặt phẳng song song

Định nghĩa 2

Cho đường thẳng a song song với mặt phẳng (a). Khoảng cách giữa đường thẳng a và mặt phẳng (a) là khoảng cách từ một điểm bất kì của a đến mặt phẳng (a).

Kí hiệu là d(a, (a)). Định nghĩa 3

Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.

, (d(a), (8) = d(M, (8)) với M c (0) . Kí hiệu là

d(a), (B) = d(M’, (0)) với M’ (8)

1.

.-

.

–

–

.

.

3. Khoảng cách giữa hai đường thẳng chéo nhau

Định nghĩa

– Đường thẳng c cắt và vuông góc với cả hai đường thăng a và b gọi là đường vuông góc chung của a và b.

– Khoảng cách giữa hai đường thẳng chéo nhau a và b chính là độ dài đoạn vuông góc chung của hai đường thẳng chéo nhau a và b. Nhận xét

. Khoảng cách giữa hai đường thằng chéo nhau bằng:

– Khoảng cách từ một trong hai đường thăng đã cho đến mặt phăng Song song với nó và chứa đường thẳng còn lại.

– Khoảng cách giữa hai mặt 0 phẳng song song lần lượt chứa hai đường thăng đó.

pa’ B.

Cách xác định đường vuông góc chung của hai đường thẳng chéo nhau

– Dựng mp (P) chứa b và song song với a.

– Từ một điểm M trên a, dựng đường thẳng vuông góc với (P), cắt (P) tại M’.

– Trong mp (P), từ M dựng . / đường thẳng a’ // a, cắt b tại B.

– Trong mp (a, a’), từ B dựng đường thẳng song song với MM’, cắt a tại A. AB là đường thẳng cần dựng.

Cách tính khoảng cách giữa hai đường thẳng chéo nhau:

– a và b là hai đường thẳng chéo nhau và a 1 b.

+ Ta dựng mặt phẳng (a) chứa a và vuông góc với b tại điểm B.

+ Trong mp (a) dựng BA I a

La

E

tại A.

b

B.

+ Ta được đoạn AB. Độ dài 1, đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.

– a và b là hai đường thẳng chéo nhau nhưng không vuông góc với nhau. Cách 1: + Ta dựng mặt phẳng (a) chứa a và song song với b.

+ Lấy một điểm M bất kì trên b, dựng MM’ vuông góc (0) E tại M’. + Từ M’ dựng bi/ b cắt a

O!! cat a E tại A.

+ Từ A dựng AB // MM’ cắt b tại B, độ dài đoạn AB là khoảng cách giữa hai đường thằng chéo nhau a và b.

Cách 2: + Ta dựng mặt phẳng (3) I a tại 0, (a) cắt b tại I.

+ Dựng hình chiếu vuông góc của b là b’ trên (a).

+ Trong (a), vě OH i b’,Heb’.

+ Từ H dựng đường thẳng song song với a cắt b tại B.

+ Từ B dựng đường thẳng song song với O{ cắt a tại A.

+ Độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.

:/:o /

1. e) Sai.
2. HƯỚNG DẪN GIẢI BÀI TẬP (SGK) Bài 1 (Trang 119, SGK)
3. a) Sai; . b) Đúng; c) Đúng: d) Sai; Bài 2 (Trang 119, SGK)
4. a) Gọi E là giao điểm của BC và AH. Khi đó AE 1 BC. Vì SA l (ABC) nên SA 1 BC.

BC I SA ‘?BC I AE

= BC I (SAE) = BC I SE. Vậy ba đường thẳng AH, SK và BC đồng quy tại điểm E. AI VI BH 1 SA nên BH 1 (SAC). b) (BH LAC he

S Mà SC c (SAC) suy ra BH 1 SC.

Mặt khác BKI SC nên SC I (BIK).

HK < (BHK) = SC 1 HK. (1)

.

.

.

(BCI (SAE) > BC I HK.

.

(2)

—

(HK C (SAE) | Từ (1) và (2) suy ra HIK I (SBC).

1. c) Ta có: AF I BC và AEI SA.

Vậy AE là đường vuông góc chung của BC và SA. Bài 3 (Trang 119, SGK)

Gọi I là hình chiếu của B trên đường chéo AC’ của hình lập phương. BCC’B’ là hình vuông cạnh a nên ta có độ dài đường chéo BC’ là a/2.

E

. Tam giác ABC là tam giác vuông tại B có BC’ = a/2 và AB = a.

Độ dài đường cao BỊ là khoảng cách từ B tới đường thẳng AC’.

Do đó:.

1 1 1 1 1 3 BI – AB? *BC*?a? + 2a + 2a

D’

ht

Suy ra: B = a 16

B

.

.

3

.

Khoảng cách từ các điểm B, C, D, A, B và D đến đường chéo AC đều bằng nhau vì chúng đều là độ dài đường cao của các tam giác vuông bằng nhau (vì có hai cạnh góc vuông tương ứng bằng nhau và đều bằng a). Bài 4 (Trang 119, SGK)

1. a) Trong mp (ABCD) kẻ BH vuông góc với AC tại H. ( BH 1 CC nên BH 1 (ACC’A’). WIBH 1 AC”

Khi đó độ dài đoạn BH chính là khoảng cách từ B tới mặt phẳng (ACC’A’). Xét tam giác vuông ABC, ta có:

Pilt 1 BH AI B BC

c

D.

–

–

b

.

a’b?.

=> BH = LTD

BH-_ab

.

B’

. b) Mặt phẳng (ACC’A’) chứa

AC’ mà AC’ song song với BB’ nên khoảng cách giữa BB’ và AC’ chính là độ : dài đoạn BH.

ab

.

BH = _ ab

w

Va? + b Chú ý: Khoảng cách giữa hai đường thẳng chéo nhau a và b bằng khoảng cách giữa a và mp (a) chứa b đồng thời song song với a. .

C’ 1 (BB’D’D). Ali

.

(1)

Die

|

Bài 5 (Trang 119, SGK)

1. a) Vì ABCD.A’B’C’D’ là hình lập .. phương nên ta có:

SA’C’ I B’D’ = AC’ I (BB’D’D). A LA’C’ I DD’ | Mà B’D c (BB’D’D) nên A’C’ 1 BD.

Mặt khác: SBC’ I B’C PCI DORIAN

C’ I (DCB’A’). (BC’ I DC B’D C (DCB’A’) = B’DI BC’. (2) Từ (1) và (2) suy ra B’D 1 (A’BC’).

1. b) Hai mặt phẳng (A’BC’) và (ACD) cùng vuông góc với B’D (tại G và H) nên chúng song song với nhau.

Khoảng cách giữa chúng là độ dài đoạn HG. Gọi độ dài cạnh hình lập phương là a.

(B’DI (BAC) – B’D I GO’.

GR

GRE

(GO’ C (BA’C’) Hai tam giác vuông G0’B’ và D’DB đồng dạng với nhau (g.g) nên ta có:

av2 GB’ O’B’ D’B’ B’D

a3 Suy ra GB = BD. Chứng minh tương tự ta có: HDBD.

Vậy HG = BD ya

1. c) Khoảng cách giữa hai đường thẳng chéo nhau BC và CD bằng khoảng cách giữa hai mặt phẳng song song (BA’C’) và (ACD’) lần lượt chứa

hai đường thẳng chéo nhau đó. Suy ra khoảng cách giữa hai đường thẳng | BC’ và CD’ là:

d(BC”, CD’) = d((BA’C’), (ACD”) = ax3

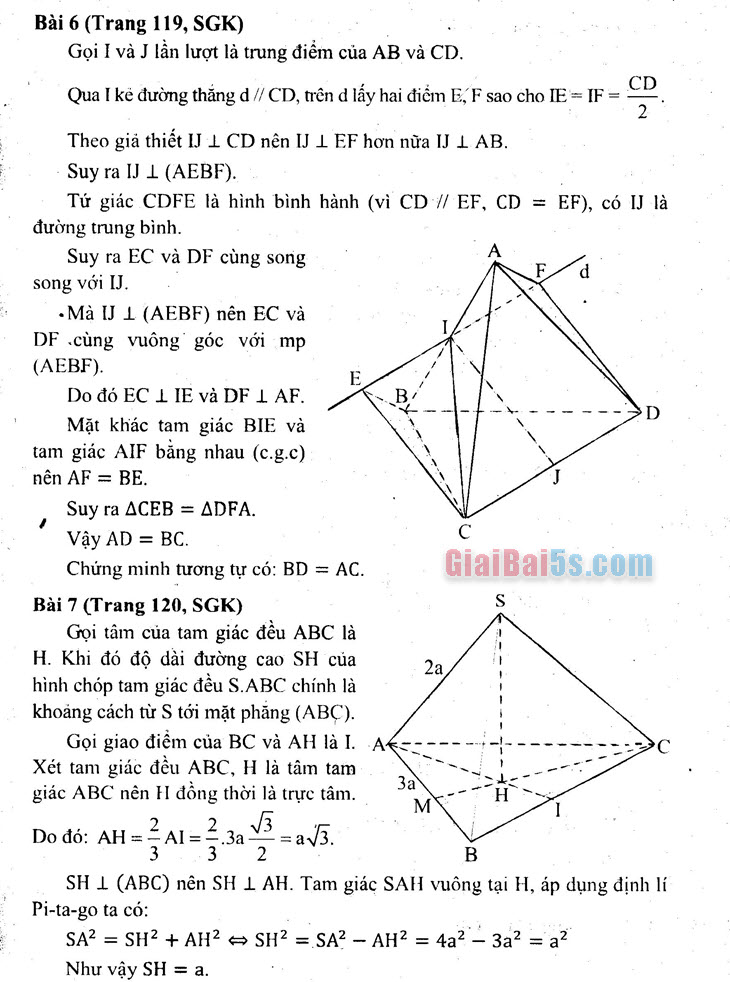
Bài 6 (Trang 119, SGK)

Gọi I và J lần lượt là trung điểm của AB và CD. Qua kẻ đường thẳng d // CD, trên d lấy hai điểm E, F sao cho IE= IF=

weit

–

–

–

–

—

–

D

Theo giả thiết IJi CD nên IJI EF hơn nữa IJI AB. Suy ra IJ 1 (AEBF).

Tứ giác CDFE là hình bình hành (vì CD // EF, CD = EF), có IJ là đường trung bình.

Suy ra EC và DF cùng song song với IJ. | Mà IJ 1 (AEBF) nên EC và

DF cùng vuông góc với mp (AEBF). | Do đó ECI IE và DF 1 AF.

Mặt khác tam giác BIE và tam giác AIF bằng nhau (c.g.c) nên AF = BE.

Suy ra ACER = ADFA. Vậy AD = BC.

Chứng minh tương tự có: BD = AC. Bài 7 (Trang 120, SGK)

Gọi tâm của tam giác đều ABC là H. Khi đó độ dài đường cao SH của hình chóp tam giác đều S.ABC chính là khoảng cách từ S tới mặt phẳng (ABC).

Gọi giao điểm của BC và AH là I, AK Xét tam giác đều ABC, H là tâm tam .. giác ABC nên đồng thời là trực tâm.

1. ME Do đó: AH = Al= 3a =a/3.

3 …3 SH 1 (ABC) nên SH 1 AH. Tam giác SAH vuông tại H, áp dụng định lí Pi-ta-go ta có:

SAP = SH2 +AH2 – SH2 = SA? – AH2 = 4a2 – 3a2 = a2 Như vậy SH = a.

.

:

D

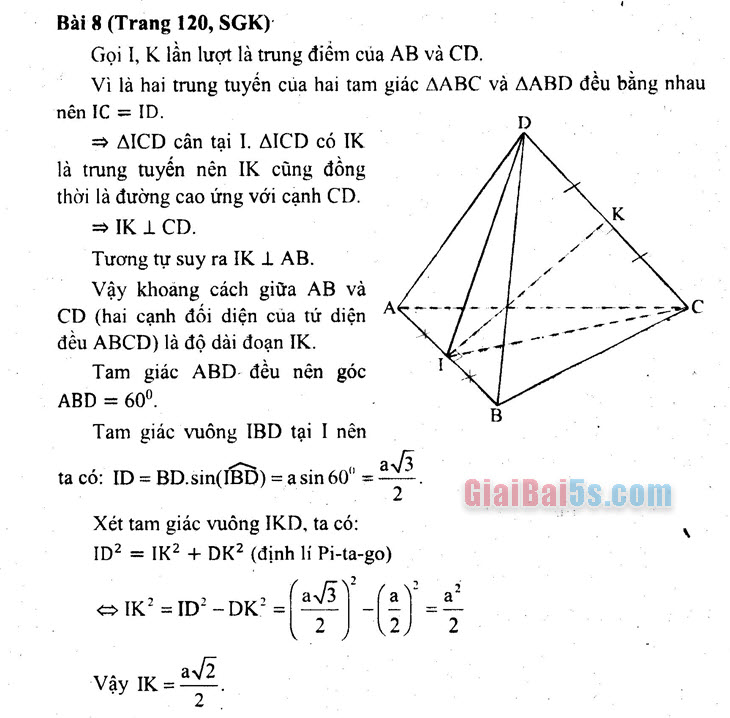
Bài 8 (Trang 120, SGK)

Gọi I, K lần lượt là trung điểm của AB và CD. * Vì là hai trung tuyến của hai tam giác AABC và AABD đều bằng nhau nên IC = ID.

| = AICD cân tại I, AICD có IK là trung tuyến nên IK cũng đồng thời là đường cao ứng với cạnh CD.

/ – IKI CD. | Tương tự suy ra IK 1 AB.

Vậy khoảng cách giữa AB và CD (hai cạnh đối diện của tứ diện As đều ABCD) là độ dài đoạn IK.

Tam giác ABD đều nên góc ABD = 60°

Tam giác vuông IBD tại I nên ta có: ID = BD.sin(IBD) = a sin 60″ = 21.

..

.

2

Xét tam giác vuông IKD, ta có: ID = IK + DK2 (định lí Pi-ta-go)

* IK*=1Do DK* – () – 3) 12 Vậy IK = ay?