1. CÂU HỎI ÔN TẬP CHƯƠNG III

. Học sinh xem lại Kiến thức cơ bản của các bài trong Chương III. II. BÀI TẬP ÔN TẬP CHƯƠNG III Bài 1 (Trang 121, SGK)

1. a) Đúng. b) Đúng.

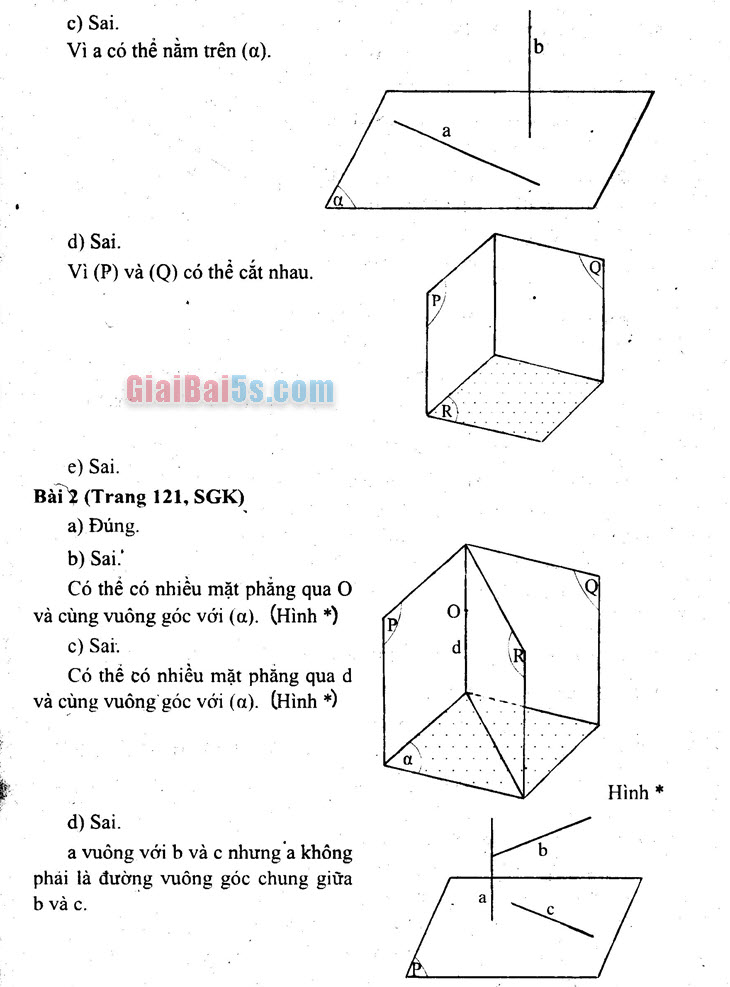
1. c) Sai. Vì a có thể nằm trên (a).
2. d) Sai. Vì (P) và (O) có thể cắt nhau.
3. e) Sai. Bài 3 (Trang 121, SGK)
4. a) Đúng. b) Sai.

Có thể có nhiều mặt phẳng qua 0 và cùng vuông góc với (a). (Hình *)

1. c) Sai.

Có thể có nhiều mặt phẳng qua di và cùng vuông góc với (a). (Hình *)

1

R

.

…

.

….

Hình *

1. d) Sai. Ta vuông với b và c nhưng a không phải là đường vuông góc chung giữa b và c. .

–D

K-.—

Ta có: {BD 1 AC

Bài 3 (Trang 121, SGK)

1. a) Theo giá thiết SA l (ABCD). Do đó ta có: SA I AB và SA I AD.

Suy ra hai tam giác SAB và SAD là / hai tam giác vuông tại A. . . | Mặt khác SA 1 (ABCD) nên AB là .. hình chiếu của SB trên mp (ABCD). . Mà BC 1 AB nên BC 1 SB (vuông –

góc với hình chiếu thì vuông góc với • đường xiên).

Tương tự ta có: CDI SD. Do đó, hai B tam giác SBC và SCD là hai tam giác vuông. – Vậy các mặt bên của hình chóp đều là các tam giác vuông. b) ABCD là hình vuông nên hai đường chéo AC và BD vuông góc.

= BD I (SAC) W.IBD I SA Do đó BD | SC. Mà SC I (a) nên SC 1 B’D.

lai đường thẳng BD và B’D’ cùng nằm trong mp (SBD) và cùng vuông góc với SC. VÌ S không vuông góc với (SBD) nên hình chiếu của SC trên mp (SBD) sẽ vuông góc với BD và B’D’. Suy ra BD // BD’. Ta có: BD (SAB) = BC 1 AB’. (1)

SC I (a) = SCIAB’. (2) Từ (1) và (2) suy ra AB’ 1 (SBC) và AB’ 1 SB. Bài 4 (Trang 121, SGK)

1. a) Theo giả thiết So I (ABCD) nên so I BC. (1)

ABCD là hình thoi nên ABCD là tam giác cân tại B. Mà góc BAD = BCD = 60° nên ABCD là tam giác đều.

Vì ABCD là tam giác đều nên DE là đường trung tuyến nên cũng là đường cao ứng với BC. Suy ra DE 1 BC. .

Xét tam giác BDE có O, F là trung điểm của BD và BE. Suy ra OF là đường trung bình của tam giác BDE. Do đó OF // DE.

Do đó OF I BỘ (2) Từ (1) và (2) suy ra BC 1 (SOF). Vậy (SBC) 1 (SOF).

 

1. b) Trong mp (SOF) dựng OIL SF (H SF) in SBC I (SOF) .am primi

nên BC 1 OH. WOH (SOF)” Suy ra OH I (SBC).

Xét tam giác SOF vuông tại 0 (Vì SO 1 (ABCD) nên F SO 1 OF) ta có:

.

.

OF = DE

V3

2

4

Е не

в

–

–

–

OH

OF ‘OS? – 1616 64

3a 9a 9a.

60)

→ OH = Ja

D . Vậy khoảng cách từ 0 đến mp (SBC) là a Gọi I là giao điểm của OF và AD. Trong mp (SIF) dựng IK I SF (FE SF. Vi AD // BC (Do ABCD là hình thoi) nên AD !! (SBC).

Khoảng cách từ A đến mp (SBC) cũng bằng khoảng cách từ 1 (1 + AD) đến mp (SBC).

BC I (SOF) nên BC 1 IK (İK C (SOF)). Suy ra IK là khoảng cách từ A đến mp (SBC). IK – 20H = 3a

Bài 5 (Trang 121, SGK)

1. a) Theo gia thiết (ABC) (ADC) với AC là giao tuyến chung, BA 1 AC suy ra BA I(ADC).

Do đó AABD là tam giác vuông tại A.

Theo định lí ba đường vuông góc, ta có BA 1 (ACD), AD 1 CD nên BDICD – Do đó ABCD là tam giác vuông tại D.

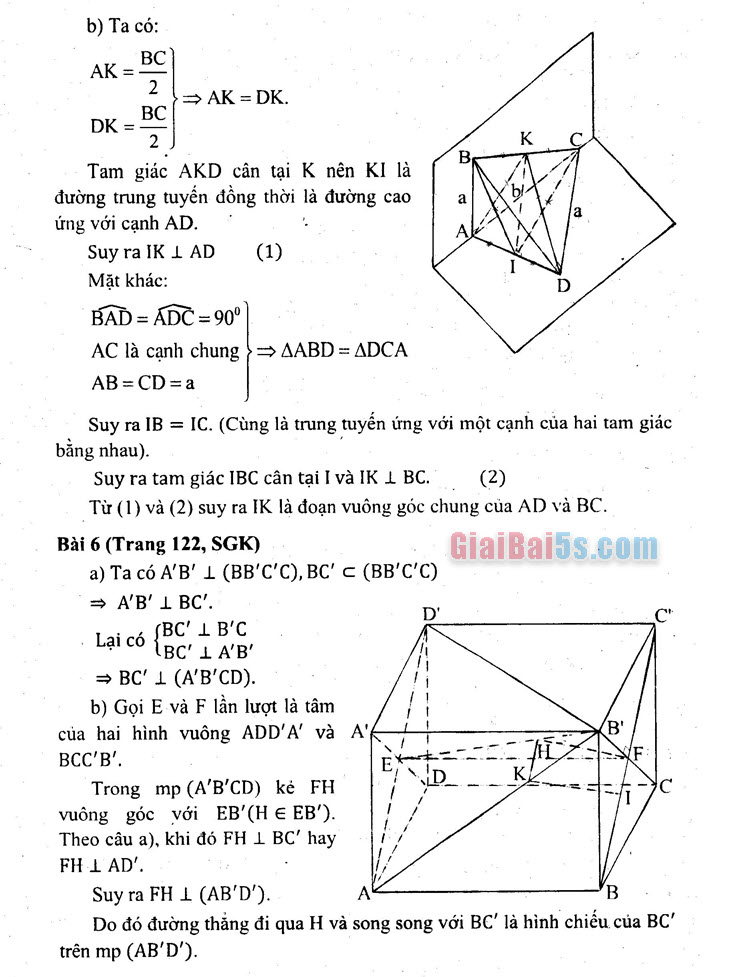
1. b) Ta có:

AK =

– BC)

>> AK = DK.

DK =

BR Tam giác AKD cân tại K nên KH là 1 đường trung tuyến đồng thời là đường cao | a| ứng với cạnh AD.

Suy ra IK I AD Mặt khác: BAD = ADC = 90° AC là cạnh chung >= AABD = ADCA AB=CD=a

Suy ra IB = IC. (Cùng là trung tuyến ứng với một cạnh của hai tam giác bằng nhau).

Suy ra tam giác IBC cân tại I và IKI BC. (2)

Từ (1) và (2) suy ra IK là đoạn vuông góc chung của AD và BC. Bài 6 (Trang 122, SGK)

1. a) Ta có A’B’ 1 (BB’C’C), BC’ c (BB’C’C) -= A’B’ I BC’.

Lại có {BC’ 1 BẮC

. Lai co (BC’ I A’B’

= BC’ I (A’B’CD)…, . b) Gọi E và F lần lượt là tâm của hai hình vuông ADD’A’ và A’

1 4 BCC’B’.

Trong mp (A’B’CD) kẻ FH vuông góc với EB’CH € EB”). Theo câu a), khi đó FH 1 BC’ hay FH I AD’. Suy ra FH I (AB’D’).

‘B . ” Do đó đường thẳng đi qua H và song song với BC là hình chiếu của BC trên mp(AB’D’).

| Đường thẳng đó cắt AB’ tại K.

Từ K kẻ KI song song với HF và cắt BC tại I. Ta có JK là đoạn vuông góc chung của AB’ và BC’. – BCC’B’ là hình vuông cạnh a nên đường chéo BC = a/2. F là tâm hình vuông BCC’B’ nên BF = BC = a2

2 2 Xét tam giác vuông B’EF ta có:

FH2 EF?

R’F2

Mà IK = FH nên IK =

Bài 7 (Trang 122, SGK)

1. a) Vì ABCD là hình thoi nên AB = BC = CD = DA. Ở BAD = 60° = AABD là tam giác đều.

[AB = AD | Tứ giác SABD có ABD là tam giác đều, SA = SB = SD nến là hình chóp tam giác đều S.ABD. . Gọi H là tâm đường tròn ngoại tiếp tam giác đều ABD. . Khi đó SH I (ABD).

Xét tam giác vuông SAH ta có:

SAP = SH2 + AH2 (Định lí Pi-ta-go) → SH = SA? – AH

3a? a? Sa?

3 :12

:

SH” + AH2

→ SH = avis.

B

Như vậy khoảng cách từ S đến mp (ABCD) là độ dài đoạn SH và bằng

a15. Lại có HC = OH + OC =

a.

Xét tam giác vuông SHC ta có:

ta

SCP = SH’ + HC2 – Sa’ 4a? Za?

1237 SC

1. b) Ta có: H + AC = SH C (SAC).. Vi SH 1 (ABCD) nên (SAC)1 (ABCD). c) SB: + BC = 3a“ ta’ – 7a“ =SC

.

–

4

4

Suy ra tam giác SBC vuông tại B. Vậy SBI BC. d) BD là giao tuyến giữa mp(SBD) và mp(ABCD).

Vì AC và BD là hai đường chéo của hình thoi ABCD nên AC 1 BD hay OH I BD.

SH I (ABCD) nên SH 1 BD. Suy ra góc p (góc SoH) là góc giữa hai mặt phẳng (SBD) và (ABCD). Vây tano-SH_av15.6.

= 15. OH6a73

III. CÂU HỎI TRẮC NGHIỆM CHƯƠNG III. 1. Chọn (C).

Ỗ Vì AB = -2ẠC + 5AD nên A, B, C và D đồng phẳng. 2. Chọn (D).

Vì AB + BỒ + CD + DÃ = AA = 0 luôn đúng với mọi A, B, C và D. . 3. Chọn (A).

2. EG = EF. EG = a. a 2. cos45o = a?

:

.

EK

Ek

LBL

с

4. (A) Sai (hình 1);

(C) Sai (hình 3);

(B) Đúng (hình 2); (D) Sai (hình 4).

habib

.

Hình 3

Flình 4

| Hình 1

Hình 2 5. Chọn (D). Hình 5.

s

.

.

.

bi

:

11ình 6

.

.

.

.

6. Chọn (D).

Hinh 5

7. Chọn (D). Hình 6. 8. Chọn (A).. 9. Chọn (D). 10. Chọn (A). 11. Chọn (B). | ABCD là tứ diện đều cạnh a. Lấy M, N là trung điểm của AB và CD.

– Xét AANB có AN = BN =

-.

D

#AANB cân tại N.

BK-ta MN là đường trung tuyến nên đồng thời là \ ! đường cao ứng với AB. Do đó MN1 AB.

Chứng minh tương tự ta có MN 1 CD. Độ dài đoạn MN chính là khoảng cách từ AB đến CD. Xét tam giác vuông BMN có: BN2 = BM? + MN2 (định lí Pi-ta-go)

MN? – BN-BM2 – 3a“ a“ _a“

–

4

4

4

Váy MN = ay?