I. KIẾN THỨC CẦN NHỚ
|




Nguồn website giaibai5s.com
Ví dụ 10: Trình bày cách vẽ rồi tính cạnh của hình vuông, hình lục giác đều, tam giác đều theo bán kính R của đường tròn ngoại tiếp mỗi hình đó.
Giải:
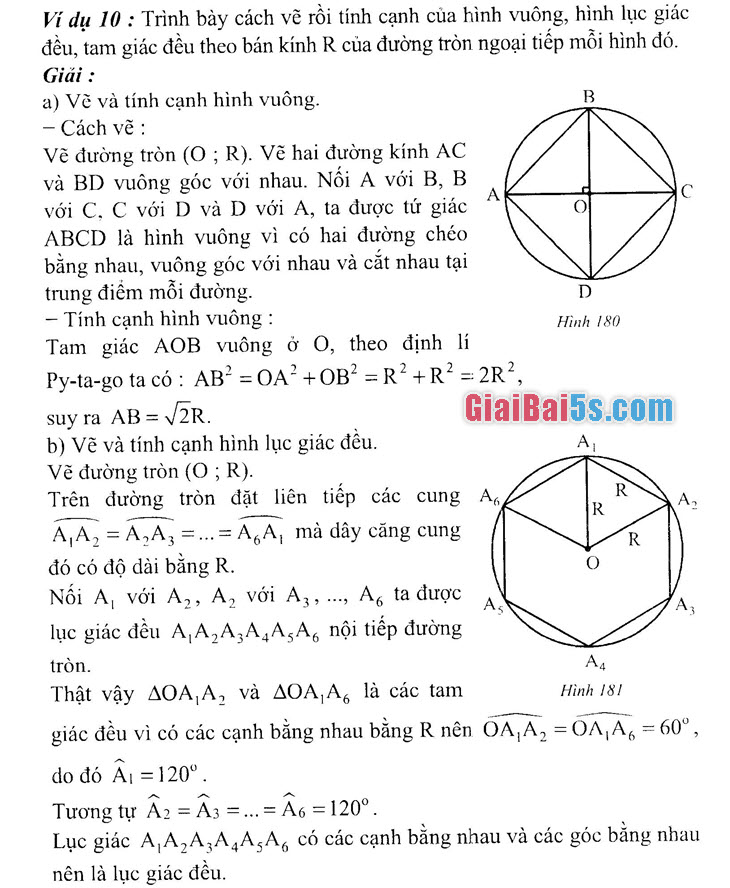
a) Vẽ và tính cạnh hình vuông.
– Cách vẽ : Vẽ đường tròn (O; R). Vẽ hai đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D và D với A, ta được tứ giác ABCD là hình vuông vì có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
– Tính cạnh hình vuông :
Tam giác AOB vuông ở O, theo định lí Py-ta-go ta có :
AB? =0A2OB^ = R^ +Ro = 2R2, suy ra AB = 2R.
b) Vẽ và tính cạnh hình lục giác đều.
Vẽ đường tròn (O; R). Trên đường tròn đặt liên tiếp các cung A AA = A,A, =.= A A, mà dây căng cung đó có độ dài bằng R. Nối A, với A2, A, với A,, …, A, ta được lục giác đều AA AA,AA, nội tiếp đường tròn. That vay ΔΟΑ,A, va ΔΟΑ,Α, 1a là tam giác đều vì có các cạnh bằng nhau bằng R nên OA,A, =0AA = 60°, do đó A =120°.
Tương tự A2 = AB =.=A6 =120°. Lục giác AA,A,AA,A, có các cạnh bằng nhau và các góc bằng nhau nên là lục giác đều.
c) Vẽ và tính cạnh của tam giác đều.
– Cách vẽ: Vẽ các điểm A, A,,…, A, như câu b (h.181).
Nối các điểm chia cách nhau một điểm ta được tam giác đều, chẳng hạn tam giác AjAzA, (h.182).
Thật vậy, theo cách vẽ ta có :
A,A,Az = A,A,A, = AŞA, A
Nên A, Az = AzAs = AŞA,
Do đó AAA,A, là tam giác đều.
Η – Tính cạnh của tam giác
A4 0 là tâm đường tròn ngoại tiếp tam giác đều AA, nên 0 là giao điểm của các đường trung trực và 0 cũng là giao điểm của các đường trung tuyến. AD cắt A,A, ở H, ta có:
OA = R ; OH = và HA = A,A = 4
(đặt A,Az = AzAg = AŞA, =
a). Tam giác AHA, vuông ở H, ta có:
A, Až = HAŽ +HA?
Ha? =*+(+ 4a?=a? +9R?
Ha? = 3R? $a = RV3.
II. BÀI TẬP
49. Trên một đường tròn (O; R), ta lần lượt đặt theo cùng một chiều, kể từ điểm A, cung AB=90°, cung BC = 45°, cung CD=45° và cung DE = 60°
a) Tính độ dài các dây cung AB, BC, CD, DE và EA theo R ;
b) Tính diện tích ngũ giác ABCDE theo R.
50. Cho hình thang ABDC (AB // DC) nội tiếp đường tròn (O; R). Biết cung CD = 60°, cung AB=120°.
a) Chứng minh tam giác AIB là tam giác vuông cân ;
b) Tính diện tích các tam giác AIB và CID theo R ;
c) Kẻ IHL AC. Tính IH theo R.
51. Cho hình vuông ABCD. Trên cạnh AB lấy hai điểm A, A, sao cho AA = A,A, = A,B; trên cạnh BC lấy hai điểm B , B, sao cho BB = BB = B,C; trên cạnh CD lấy hai điểm C, C, sao cho CC =CC, =C,D và trên cạnh DA lấy hai điểm D, D, sao cho DD, =D,D2 = D,A.
a) Chứng minh hình bát giác AA.BB.CC, DD, nội tiếp được đường tròn ;
b) Hình bát giác AA,B,B,CC,DD, có phải là đa giác đều hay không ? Vì sao ?
52. Cho tam giác đều ABC nội tiếp đường tròn (O; R), đường kính AD. Gọi E là trung điểm của cạnh AC, tia DE cắt đường tròn ở F.
a) Tính BE, DE theo R;
b) Chứng minh AEDC – AEAF;
c) Tính EF, AF theo R.
III. HƯỚNG DẪN GIẢI – ĐÁP SỐ
Oi 90
49. a) AE = 360° – (AB+BC+CD+DE)
= 360° – (90° +45° +45° +60°)
= 120°. AAOB vuông cân ở 0 :
AB = OA^ + OB = 2R? suy ra
AB=RV2. Gọi giao điểm của OC và BD là H. Ta dễ dàng chứng minh được BD=R2 và
PUL BD RV2 OCTBD tại H và BH ===
60
145
Hình 183
Tam giác OHB vuông cân ở H, ta có
-, do đó
HC =0C-OH=R – RV2 = R(2-v2)
Trong tam giác vuông BHC, ta có :
BC°= Bu + HC =(R2) • [R42=17)] = (2-v2ir?
R
R
RV
SAOB = —
;
= SCOL
AOE
2
suy ra BC = R2-M2 = CD. AOED là tam giác đều, ED= R. Góc AOE =120° nên AE chính là cạnh của tam giác đều nội tiếp đường tròn (O; R), do đó AE = R 3.
b) Bạn đọc hãy chứng minh.
R2 Saan = ; Smoc =Scoo =R_v3.; Srov = R2,43 ; Sok = REVI Do đó SABCDE = SAOB + Sboc +Scop +Spoe + SEOA
= (3. 9) 15 + 12+ 50. a) Ta có :
AD=CB = 360° – 60° +120° = 90° Pz60° TAB = -s« CB = L 90o = 45°
60°
AD – CB=3600_
o 60° +120°
– = 90° 2
7° = 45°
a
IBA = =s
0° = 45°.
00
120°
Tam giác AB có IAB=IBA = 45° nên là C tam giác vuông cân ở I.
b) AB=120° nên AB là cạnh của tam giác đều nội tiếp đường tròn (O; R), do đó
Hình 184 AB = RV3. Tam giác AIB vuông ở I:
IA? + IB? = AB, suy ra 2IA? = 3RẺ, do đó IA2 =2^
Sam = 19.1B =-14 2 – BR
AIB
Chứng minh tương tự, tam giác CID vuông cân ở I và SCD =.
ICDR2
c) CAD = SACD = _.60o = 30°.
AL R16 Tam giác AHA vuông ở H, lại có IAH = 30°, nên IH =
24
51. a) Gọi O là giao điểm hai đường chéo ACE
và BD của hình vuông ABCD, ta có : AOAA, = AOBA, (c.g.c),
suy ra OA, = 0A, AOBA, =AOBB (c.g.c),
suy ra OA2 = OB,
Tương tự: OB = OB,…, OD, = OA,
Do đó OA = OA = OB = OB, =OC D C, C c =OC2 = OD, = OD2
Vậy tám điểm A, A2, B1, B2,C, C, D, D, cùng nằm trên một đường tròn tâm O, bán kính OA,..
b) Dễ thấy các góc : = 2 = ß1 = B2 = ĉi = ĉ2 = Ô = Ô2 = 135°
Đặt cạnh hình vuông bằng a, ta có : AA, =. Trong tam giác vuông cân A,BA, , ta có : (A,B) = (BA) +(BB) = 2a’ suy ra A,B = 2 Rõ ràng AA, + A,B,. .
Đa giác AA,C,C,DD, có các góc bằng nhau nhưng các cạnh không bằng nhau nên không là đa giác đều.
Chú ý : Đa giác đều thì nội tiếp được đường tròn, nhưng một đa giác nội tiếp đường tròn không nhất thiết phải là đa giác đều.
IV
9
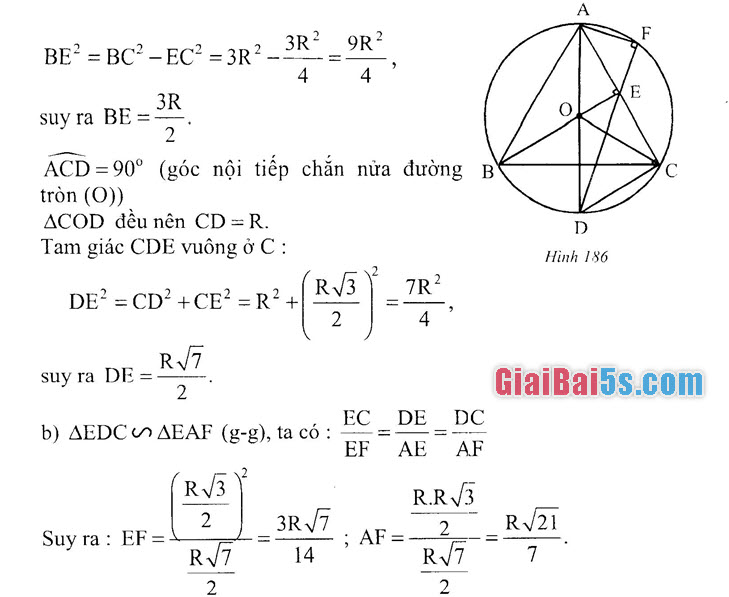
52. a) BC là cạnh của tam giác đều ABC nội tiếp đường tròn (O; R) nên
BC =R/3. (ví dụ 1c)). E là trung điểm của AC nên BE I AC và CE =2 Tam giác BEC vuông ở E:
23R29R? BE? = BCP – EC2 = 3R2 – 3
44,
suy ra BE =3R
ACD = 90° (góc nội tiếp chắn nửa đường B tròn (O)) ACOD đều nên CD = R. Tam giác CDE vuông ở C:
D
Hình 186
7R?
DE” = CD+CE = R2 +
suy ra DE =
EC DE DC b) AEDCU AEAF (g-g), ta có :
EF AE AF
–
=
(R/3 2
R.Rs
3R17
2
Suy ra : EF =
RV21
2 I RVT
; AF =
–
=
2 RV7
2
Giải:
a) Vẽ và tính cạnh hình vuông.
– Cách vẽ : Vẽ đường tròn (O; R). Vẽ hai đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D và D với A, ta được tứ giác ABCD là hình vuông vì có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
– Tính cạnh hình vuông :
Tam giác AOB vuông ở O, theo định lí Py-ta-go ta có :
AB? =0A2OB^ = R^ +Ro = 2R2, suy ra AB = 2R.
b) Vẽ và tính cạnh hình lục giác đều.
Vẽ đường tròn (O; R). Trên đường tròn đặt liên tiếp các cung A AA = A,A, =.= A A, mà dây căng cung đó có độ dài bằng R. Nối A, với A2, A, với A,, …, A, ta được lục giác đều AA AA,AA, nội tiếp đường tròn. That vay ΔΟΑ,A, va ΔΟΑ,Α, 1a là tam giác đều vì có các cạnh bằng nhau bằng R nên OA,A, =0AA = 60°, do đó A =120°.
Tương tự A2 = AB =.=A6 =120°. Lục giác AA,A,AA,A, có các cạnh bằng nhau và các góc bằng nhau nên là lục giác đều.
c) Vẽ và tính cạnh của tam giác đều.
– Cách vẽ: Vẽ các điểm A, A,,…, A, như câu b (h.181).
Nối các điểm chia cách nhau một điểm ta được tam giác đều, chẳng hạn tam giác AjAzA, (h.182).
Thật vậy, theo cách vẽ ta có :
A,A,Az = A,A,A, = AŞA, A
Nên A, Az = AzAs = AŞA,
Do đó AAA,A, là tam giác đều.
Η – Tính cạnh của tam giác
A4 0 là tâm đường tròn ngoại tiếp tam giác đều AA, nên 0 là giao điểm của các đường trung trực và 0 cũng là giao điểm của các đường trung tuyến. AD cắt A,A, ở H, ta có:
OA = R ; OH = và HA = A,A = 4
(đặt A,Az = AzAg = AŞA, =
a). Tam giác AHA, vuông ở H, ta có:
A, Až = HAŽ +HA?
Ha? =*+(+ 4a?=a? +9R?
Ha? = 3R? $a = RV3.
II. BÀI TẬP
49. Trên một đường tròn (O; R), ta lần lượt đặt theo cùng một chiều, kể từ điểm A, cung AB=90°, cung BC = 45°, cung CD=45° và cung DE = 60°
a) Tính độ dài các dây cung AB, BC, CD, DE và EA theo R ;
b) Tính diện tích ngũ giác ABCDE theo R.
50. Cho hình thang ABDC (AB // DC) nội tiếp đường tròn (O; R). Biết cung CD = 60°, cung AB=120°.
a) Chứng minh tam giác AIB là tam giác vuông cân ;
b) Tính diện tích các tam giác AIB và CID theo R ;
c) Kẻ IHL AC. Tính IH theo R.
51. Cho hình vuông ABCD. Trên cạnh AB lấy hai điểm A, A, sao cho AA = A,A, = A,B; trên cạnh BC lấy hai điểm B , B, sao cho BB = BB = B,C; trên cạnh CD lấy hai điểm C, C, sao cho CC =CC, =C,D và trên cạnh DA lấy hai điểm D, D, sao cho DD, =D,D2 = D,A.
a) Chứng minh hình bát giác AA.BB.CC, DD, nội tiếp được đường tròn ;
b) Hình bát giác AA,B,B,CC,DD, có phải là đa giác đều hay không ? Vì sao ?
52. Cho tam giác đều ABC nội tiếp đường tròn (O; R), đường kính AD. Gọi E là trung điểm của cạnh AC, tia DE cắt đường tròn ở F.
a) Tính BE, DE theo R;
b) Chứng minh AEDC – AEAF;
c) Tính EF, AF theo R.
III. HƯỚNG DẪN GIẢI – ĐÁP SỐ
Oi 90
49. a) AE = 360° – (AB+BC+CD+DE)
= 360° – (90° +45° +45° +60°)
= 120°. AAOB vuông cân ở 0 :
AB = OA^ + OB = 2R? suy ra
AB=RV2. Gọi giao điểm của OC và BD là H. Ta dễ dàng chứng minh được BD=R2 và
PUL BD RV2 OCTBD tại H và BH ===
60
145
Hình 183
Tam giác OHB vuông cân ở H, ta có
-, do đó
HC =0C-OH=R – RV2 = R(2-v2)
Trong tam giác vuông BHC, ta có :
BC°= Bu + HC =(R2) • [R42=17)] = (2-v2ir?
R
R
RV
SAOB = —
;
= SCOL
AOE
2
suy ra BC = R2-M2 = CD. AOED là tam giác đều, ED= R. Góc AOE =120° nên AE chính là cạnh của tam giác đều nội tiếp đường tròn (O; R), do đó AE = R 3.
b) Bạn đọc hãy chứng minh.
R2 Saan = ; Smoc =Scoo =R_v3.; Srov = R2,43 ; Sok = REVI Do đó SABCDE = SAOB + Sboc +Scop +Spoe + SEOA
= (3. 9) 15 + 12+ 50. a) Ta có :
AD=CB = 360° – 60° +120° = 90° Pz60° TAB = -s« CB = L 90o = 45°
60°
AD – CB=3600_
o 60° +120°
– = 90° 2
7° = 45°
a
IBA = =s
0° = 45°.
00
120°
Tam giác AB có IAB=IBA = 45° nên là C tam giác vuông cân ở I.
b) AB=120° nên AB là cạnh của tam giác đều nội tiếp đường tròn (O; R), do đó
Hình 184 AB = RV3. Tam giác AIB vuông ở I:
IA? + IB? = AB, suy ra 2IA? = 3RẺ, do đó IA2 =2^
Sam = 19.1B =-14 2 – BR
AIB
Chứng minh tương tự, tam giác CID vuông cân ở I và SCD =.
ICDR2
c) CAD = SACD = _.60o = 30°.
AL R16 Tam giác AHA vuông ở H, lại có IAH = 30°, nên IH =
24
51. a) Gọi O là giao điểm hai đường chéo ACE
và BD của hình vuông ABCD, ta có : AOAA, = AOBA, (c.g.c),
suy ra OA, = 0A, AOBA, =AOBB (c.g.c),
suy ra OA2 = OB,
Tương tự: OB = OB,…, OD, = OA,
Do đó OA = OA = OB = OB, =OC D C, C c =OC2 = OD, = OD2
Vậy tám điểm A, A2, B1, B2,C, C, D, D, cùng nằm trên một đường tròn tâm O, bán kính OA,..
b) Dễ thấy các góc : = 2 = ß1 = B2 = ĉi = ĉ2 = Ô = Ô2 = 135°
Đặt cạnh hình vuông bằng a, ta có : AA, =. Trong tam giác vuông cân A,BA, , ta có : (A,B) = (BA) +(BB) = 2a’ suy ra A,B = 2 Rõ ràng AA, + A,B,. .
Đa giác AA,C,C,DD, có các góc bằng nhau nhưng các cạnh không bằng nhau nên không là đa giác đều.
Chú ý : Đa giác đều thì nội tiếp được đường tròn, nhưng một đa giác nội tiếp đường tròn không nhất thiết phải là đa giác đều.
IV
9
52. a) BC là cạnh của tam giác đều ABC nội tiếp đường tròn (O; R) nên
BC =R/3. (ví dụ 1c)). E là trung điểm của AC nên BE I AC và CE =2 Tam giác BEC vuông ở E:
23R29R? BE? = BCP – EC2 = 3R2 – 3
44,
suy ra BE =3R
ACD = 90° (góc nội tiếp chắn nửa đường B tròn (O)) ACOD đều nên CD = R. Tam giác CDE vuông ở C:
D
Hình 186
7R?
DE” = CD+CE = R2 +
suy ra DE =
EC DE DC b) AEDCU AEAF (g-g), ta có :
EF AE AF
–
=
(R/3 2
R.Rs
3R17
2
Suy ra : EF =
RV21
2 I RVT
; AF =
–
=
2 RV7
2
