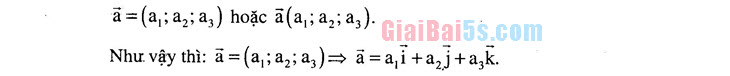1. KIẾN THỨC CƠ BẢN 1. Hệ toạ độ

| Trong không gian cho ba trục toạ độ chung gốc 0, đôi một vuông góc

M với nhau: x’Ox, y’oy, z’Oz. Hệ thống ba trục toạ độ như vậy gọi là hệ trục toạ độ Đề-các vuông góc Oxyz; 0 được gọi là gốc toạ độ. Giả sử i, j, k lần lượt là các vectơ đơn vị trên các trục xOx, yoy,zOz. 2. Toạ độ giao điểm

Trong không gian, cho hệ trục toạ độ Oxyz và một điểm M tùy ý. Khi đó i, j, k không đồng phẳng nên tồn tại duy nhất một bộ ba số sao cho OM = xi + yj + zk

Ta nói bộ ba số (x, y, z) là toạ độ của điểm M đối với hệ trục toạ độ Oxyz đã cho và viết M(x, y, z) hoặc M = (x; y; z).

Như vậy M(x,y,z) = OM = xy+yj+ zk. 3. Toạ độ của vectơ | Trong không gian Oxyz cho vectơ a, ta luôn có a = ai + a,j+a,k. Khi đó bộ ba số (a); a); ag) được xác định duy nhất và được gọi là toạ độ của vectơ ả đối với hệ trục toạ độ Oxyz. Ta viết như sau:

a =(a,; az; az) hoặc ā(a,; az; az).

Như vậy thì: a=(a; a, a,)= a=ai-a,j+a,k. 4. Biểu thức toạ độ của các phép toán vectơ

– Định lí

Đối với hệ trục Oxyz, nếu có hai vectơ a(a; a,; a, và b(bộ; b; b,) thì ta có: ā+b =(a, +b,; a+ b2; a, + b3). ā-b= (a, – b,; a, – bz; az – bz). kā = k(a,; az; az) = (ka,; kaz; kaz) với ke R. – Hệ quả Cho hai vectơ a(a ; a ; a,) và b(b; b; b,). Ta có:

a=b6a, = b; a, = by; az = bz. + Vectơ 0 có toạ độ là (0, 0, 0).

+ Với b40 thì hai vectơ a và b cùng phương khi và chỉ khi có một số k sao cho: a = kb,; az = kby; az = kbz.

+ Trong không gian Oxyz, nếu hai điểm A(XA; VA; ZA) và B(XB; MB; ZB) thì: AB = (X8 – XA; YB – YA; 25 -2). + Toạ độ trung điểm M của đoạn thẳng AB là: M=( ****p, Ya+ya,42 +29

2 2 5. Tích vô hướng (Biểu thức toạ độ của tích vô hướng)

Trong không gian Oxyz, tích vô hướng của hai vectơ (a; a; a) và b(b; b; b,) được xác định bằng công thức sau: a.b=ab +a,b, Fa,b,.

Như vậy: Cho a(a,; a,; a,), độ dài vectơ a là: a = a + a +a. Cho hai điểm A(XA; VA; ZA) và B(XB, VB, ZB). Ta có: AB =[AB = V(xp-x»)? +(Y: -JP+(29 -2? Gọi ọ là góc giữa hai vectơ a(a; a,; a,) và b(b, b, b,) với a, b = 0 thì: cosp = cos(ā;b) = al.6, Tapi tantas Joi + b} + b}

a, b, +azbą + azb? ālā= a, b, + a, b, +azb> = 0. 6. Phương trình mặt cầu

– Định lí

COSQ

CO

—

Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c), bán kính r có phương trình là:

(x – a)? + (y – b)2 + (2 – c)2 = r?.

– Phương trình dạng: x^+y+z^ +2Ax +2By+2Cz+D=0 với điều kiện A+B+C -D>0 là phương trình mặt cầu tâm I(-A; -B; -C) có bán kính bằng A2+B+C – D. B. HƯỚNG DẪN GIẢI BÀI TẬP (SGK) Bài 1 (Trang 68, SGK)

1. a) Ta có: a =(2; – 5; 3) = 4ā = (8; – 20; 12)

6 = 60; 2:- 1)=-46=(0; -31 d = 48 -36 +3+=(3+0+3 –20 – + 21;12+5+6)=(*)

© = (1; 7; 2) = 30 =(3; 21; 6)

1. b) Ta có: à = (2; – 5; 3) b = (0; 2; -1)=-45 = (0; – 8; 4) C = (1; 7; 2) –2c =(-2; – 14; -4)

ērā -46 – 27 = (2+0 – 2; -5-8-14; 3+4-4) = (0); – 27; 3). Bài 2 (Trang 68, SGK) – Cách 1:

Gọi M là trung điểm của cạnh BC. Theo công thức trung điểm của đoạn thẳng ta có:

= -(XB

+X

) =

R

MI —-

2′ 2″

C] trong tam tain giác ABC. Theo tính chất trọng tâm của tam giác, điểm 3 cách đỉnh A một đoạn AG = AM.

= AG = AM. Vi Ad: -: ), M (3 2 ) nén AM=( 1135)

2)

BAG== AM. Vì A(l; -1; 1), M) –

nên AM = -, – 12:22)

– Gọi (x; y; Z) là toạ độ của trọng tâm G. Ta có: A(1; – 1; 1), G(x; y; z)= AG=(x-1; y+l; z-1). Theo điều kiện bằng nhau của hai vectơ ta có:

x-1=

AG = AM ={y+l=} ({}) ={y=8

1

y +1 =

Cách 2: Gọi (x, y, z) là toạ độ trọng tâm G của tam giác ABC. Ta có: GA = (1-x;-1-y;1- z); GB = (-x;1-y; 2-z); GC = (1 – x; -y; 1-z). = GA+GB+GC = (2 – 3x; – 3y; 4 – 32). Mà G là trọng tâm nên GA 4GB+GC = 0.

2-3x = 0) x =

3

Suy ra: {-3y = 0 = y = 0

4-32=1

Z=

Nhận xét:

Toạ độ trọng tâm G của tam giác ABC bằng trung bình cộng các toạ độ tương ứng của ba đình của tam giác. Bài 3 (Trang 68, SGK)

Tui

AB== (: 1; 1);

AD=(0; – 1; 0);

(xc-2 =0 (xc = 2 BC = AD = {yc-1=-1 {ys = 0

(26 -2 = 0 (2c = 2 Do đó: C=(2; 0; 2). Suy ra: CC=(2; 5; -7). Từ AA = BB =DD=CC =(2; 5; -7). xx-1=2

D(1;-1; 1) Suy ra {y – 0=5

A(1; 0; 1)/1 7 2x:-1=-7

– B(2; 1; 4) xx=3 > {yx = 5

C'(4; 5; -5) 12x = -6 Vậy A =(3; 5;-6).

Chứng minh tương tự ta có: B =(4; 6; -5) và D =(3; 4;-6). Bài 4 (Trang 68, SGK)

3. a) Theo công thức toạ độ của tích vô hướng giữa hai vectơ, ta có: a.b= 3.2+0.(-4)+(-6).0=6. b) Chứng minh tương tự, ta có:

c.d = 1.4+(-5).3+2.(-5)=-21. Bài 5 (Trang 68, SGK) | Phương trình mặt cầu có dạng:

x2 + y2 +2? + 2Ax + 2By + 2Cz+D = 0

Với A +Bo+C –D>0 thì có tâm I(-A; -B; -C) và có bán kính r=VA? +B’ +C? -D.

1. a) Ta có: 2A=-83-A=4; 2B=-23-B=1; 2C=0>C=0; D = 1. =I(4; 1; 0) và r = 4. Vậy mặt cầu có tâm I(4; 1; 0) và bán kính r= 4.

B’

Chú ý: Ta có thể đưa phương trình mặt cầu về dạng:

(x-a)? +(y-b)2 +(2-c)? =r? Để có tâm I(a; b; c). Muốn vậy ta sử dụng các hằng đẳng thức đáng nhớ để chuyển các bình phương thiếu trở thành các bình phương của nhị thức.

Ta có: x2+y+z? – 8x – 2y +1 = 0 + x – 8x + y^ – 2y+z^ + 1 = 0.

Ta nhận thấy x2 – 8x là một bình phương thiếu nên ta thêm và bớt đi một hạng tử thứ ba để làm xuất hiện một bình phương của nhị thức:

x2 — 8x = x2 – 8x +16-16 = (x – 4)2 – 16. Tương tự như vậy ta có:

y2 — 2y = y2 – 2y+1-1=(y-1)2 – 1. Như vậy phương trình mặt cầu sẽ trở thành: (x-4)2 – 16+(y-1)2 -1+2° +1=0 + (x – 4)+(y-1)2 +z? = 16. Từ đó suy ra tâm I(4; 1; 0) và bán kính r= 416 =4. b) Trước hết ta đưa về dạng quen thuộc bằng cách chia cả hai vế cho 3: 3×2 +3y2 +372 – 6x +8y +152–3=0 + xo+y+z2 – 2x + y +52–1=0. Khi đó ta có:

2A =-26-A= 1; 2B = =-=-* 2C=54-C= D=-1. Như vậy (1- 3) và bán kính là: =y=+*+6) +(=(-1) – V

Bài 6 (Trang 68, SGK)

1. a) Cách 1: Gọi I là trung điểm của AB. Khi đó mặt cầu đường kính AB có tâm là I và bán kính ra

Ta có: I(3; -1; 5) và r =IA? =9. Do đó phương trình mặt cầu đường kính AB có dạng: (x – 3)2 + (y +1) + (2-5)2 = 9. Cách 2:

Mặt cầu đường kính AB là tập (S) các điểm M trong không gian nhìn đoạn AB dưới một góc vuông.

Giả sử M(x, y, z), khi đó Me (S)ệ AM ( BM = AM.BM = 0. (1) Ta có: AM = (x – 4; y+3; z-7), BM = (x – 2; y=1; z-3) (1) = (x-4)(x – 2)+(y +3)(y-1)+(z-7)(z-3)=0

x2 + y2 +z2 – 6x +2y – 102 + 26 = 0 = (x – 3)+(y + 1)+ (z – 5)2 = 9. Đây là phương trình mặt cầu mà ta cần tìm. b) Mặt cầu cần tìm có tâm C(3; –3; 1) và có bán kính r=AC = (3-5)? +(-3+2) +(1-1) = V5.

Phương trình mặt cầu cần tìm là: (x – 3)^ +(y+3)^+(2-1) =5.