| A. KIẾN THỨC CƠ BẢN
1. Phương trình đường thẳng – Phương trình tham số của đường thẳng Định lí: + Trong không gian Oxyz cho đường thẳng A đi qua điểm M (xo; yo; zo) và nhận
+ Phương trình tham số của đường thẳng A đi qua điểm M (x0; y0; z0) và có vectơ chỉ phương – Phương trình chính tắc của đường thẳng Nếu a1, a2, a3 đều khác 0 thì người ta còn có thể viết phương trình của đường thẳng Δ dưới dạng chính tắc như sau: 2. Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau Cho hai đường thẳng d và d’ lần lượt đi qua M (xo ; yo; zo), M'(x’o, y’o, z’o ) và có vectơ chỉ phương theo thứ tự là
3. Điều kiện để một đường thẳng song song, cắt hoặc vuông góc với mặt Cho đường thẳng d đi qua điểm Mo(xo; yo; zo), có vectơ chỉ phương Gọi
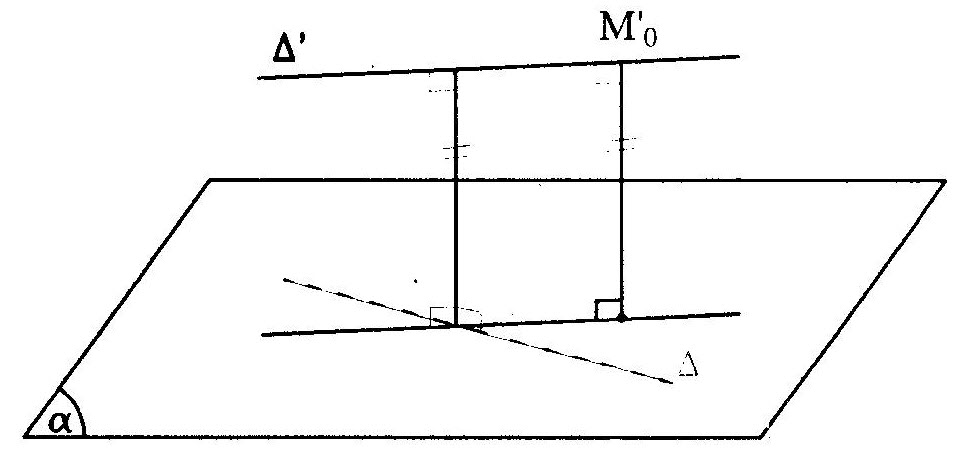
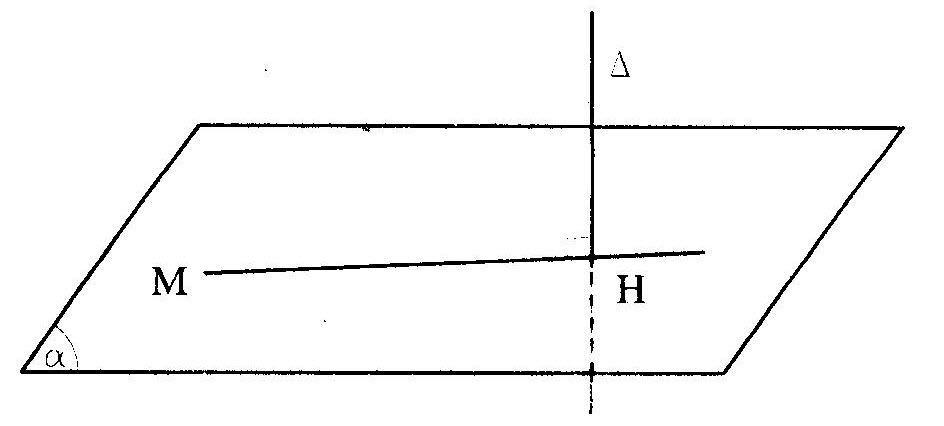
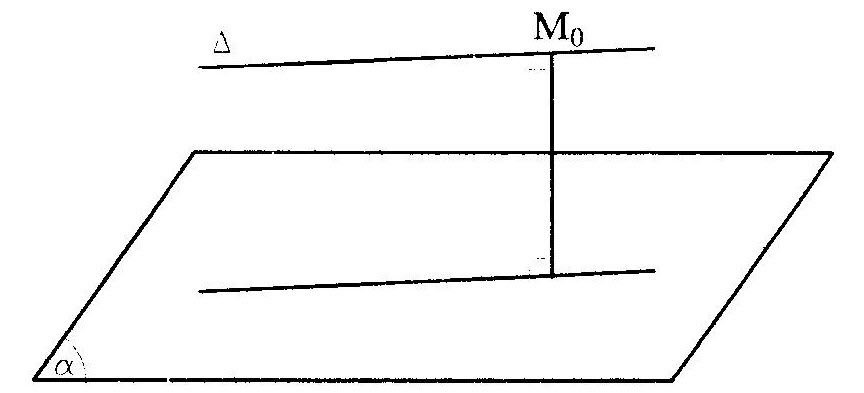
4. Tính khoảng cách – Trong không gian Oxyz, để tính khoảng cách từ điểm M đến đường thẳng Δ ta thực hiện các bước: + Viết phương trình mặt phẳng (α) chứa M và vuông góc với Δ; + Tìm giao điểm H của Δ với (α); + Khoảng cách từ điểm M đến Δ chính là khoảng cách giữa hai điểm M và H: d(M,Δ) = MH. – Để tính khoảng cách giữa đường thẳng Δ và mặt phẳng (α) song song với Δ ta thực hiện các bước: + Lấy một điểm M(x ; y ; Zn) tùy ý trên đường thẳng Δ; – Khoảng cách giữa Δ và mặt phẳng (α) là khoảng cách từ điểm Mo d(Δ,(α)) = d(M,(α)) – Để tính khoảng cách giữa hai đường thẳng chéo nhau và Δ ta thực hiện các bước: + Viết phương trình mặt phẳng (α) chứa đường thẳng Δ và song song với đường thẳng Δ’; + Lấy một điểm M’o M(x’o; y’o ; z’o) tùy ý trên Δ’; – Khoảng cách giữa Δ và Δ’ chính là khoảng cách từ điểm M’o đến mặt phẳng (α): d(Δ, Δ’)=d(Mo, (α)). |









Nguồn website giaibai5s.com
- KIẾN THỨC CƠ BẢN 1. Phương trình đường thẳng
– Phương trình tham số của đường thẳng Định lí:
+ Trong không gian Oxyz cho đường thẳng A đi qua điểm M (Xo; yo; Z0) và nhận a = (a); a2, a3) làm vectơ chỉ phương. Điều kiện cần và đủ để điểm M(x, y, z) nằm trên A là có một số thực t sao cho:
x = xo + ta, y=yo +ta,
12=Zo + taz + Phương trình tham số của đường thẳng A đi qua điểm M (X0; y0; Z0) và
x = xo + ta, có vectơ chỉ phương 4 = (a1; 22; as) là phương trình có dạng: y = y + ta,
z=2, + taz trong đó t là tham số.
– Phương trình chính tắc của đường thẳng
Nếu a1, a2, a3 đều khác 0 thì người ta còn có thể viết phương trình của đường thẳng A dưới dạng chính tắc như sau: * *0 =YCY0 =< <
a, az az 2. Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau | Cho hai đường thẳng d và do lần lượt đi qua M (x ; yo; Zn), M(x, y, z ) và có vectơ chỉ phương theo thứ tự là a=(a; a,;a,),a =(a; a; an). Gọi i=[a, J. Ta có:
í ñ=7 d // d’
M, € d’
de des Nñ=ő
M, ed’
dcắt d’s ño
Iñ.M,M=0 d và do chéo nhau = nMM + 0
didaa’ = 0. 3. Điều kiện để một đường thẳng song song, cắt hoặc vuông góc với mặt phăng | Cho đường thẳng d đi qua điểm M,(x ; y + z), có vectơ chỉ phương lã=(a; a; an) và cho mặt (a) có phương trình: Ax + 3y + Cu + D = 0.
Gọi n =(A; B; C) là vectơ pháp tuyến của (a). Ta có các điều kiện sau:
d // (a)
Jañ=7
M.€ (a)
de(a)
a=
M, e(Q) d cắt (a) = än+ dl(a) =ñ=kā.
- Tính khoảng cách | – Trong không gian Oxyz, để tính khoảng cách từ điểm M đến đường thẳng A ta thực hiện các bước: | + Viết phương trình mặt
/ Phẳng (a) chứa M và vuông góc với A;
- Tìm giao điểm H của A với (a);
+ Khoảng cách từ điểm M đến A chính là khoảng cách giữa hai điểm M và H: d(M,A) = MH.
– Để tính khoảng cách giữa đường thẳng A và mặt phẳng (3) song song với A ta thực hiện các bước:
+ Lấy một điểm M(x ; y ; Zn) tùy ý trên đường thẳng A;
– Khoảng cách giữa A và mặt phẳng (a) là khoảng cách từ điểm Mo đến raặt phẳng (a):
d(A,(a)) = d(M,,(a))
– Để tính khoảng cách giữa hai đường thẳng chéo nhau A và 4 ta / thực hiện các bước:
++ Viết phương trình mặt phẳng (d) chứa đường thẳng A và song song với. đường thẳng A’; +- Lấy một điểm
Mo M(x; y ; z) tùy ý trên A;
— Khoảng cách giữa A và A chính là khoảng cách từ điểm M, đến mặt phẳng (d):
d(A, A’)=d(M., (a)).
Mo
- HƯỚNG DẪN GIẢI BÀI TẬP (SGK) Bài 1 (Trang 89, SGK)
- a) d đi qua điểm M(5; 4; 1) và có vectơ chỉ phương a=(2; -3; 1) nên d có phương trình tham số là:
x=5+2t y=4-3t, teR. z=1+t
- b) Vì d vuông góc với mặt phẳng (d): x + y – z + 5 = 0 nên d nhận vectơ a = (1; 1; -1) làm vectơ chỉ phương. Do đó, d có phương trình tham số là: x = 2+t y=-1+t, teR. [z=3-t
x=1+2t c) Do d song song với đường thẳng A:/y=-3+3t nên d nhận vectơ
z=44 a=(2; 3; 4) làm vectơ chỉ phương. Mặt khác d đi qua B(2; 0; -3). Vậy d có
x = 2+2t phương trình tham số là: y=3t, te R.
(z=-3+41
- d) Do d đi qua P(1; 2; 3) và Q(5; 4; 4) nên d nhận vectơ PQ = (4; 2; 1) làm
(x=1+41 vectơ chỉ phương. Vậy d có phương trình tham số là: {y = 2+2t ,te R.
z= 3+1
Bài 2 (Trang 89, SGK)
Cách 1:
Lấy hai điểm trên d và tìm hình chiếu vuông góc của nó trên mặt phẳng (Oxy). Đường thẳng đi qua hai điểm đó chính là hình chiếu cần tìm. Ví dụ ta lấy M (2: _3: 1) và M (0.
y M (2; -3; 1) và Mg(0; -7; -5) cùng thuộc d. Hình chiếu vuông góc trên (Oxy) của M là điểm N (2; -3; 0), của M là điểm Ng(0; -7; 0).
Đường thẳng A đi qua N và N2 chính là hình chiếu vuông góc của d trên (Oxy). Ta có: NN,(-2; -4; 0) || V(1; 2; 0).
x = 2+t Vậy phương trình tham số của A là: {y =-3+ 2t, te R.
[z=o
Cách 2:
Xét mặt phẳng (P) đi qua d và vuông góc với (Oxy). Khi đó A = (P) (Oxy) chính là hình chiếu vuông góc của d lên mặt phẳng (Oxy).
| Phương trình mặt phẳng (Oxy) có dạng 1 = 0; vectơ pháp tuyến của (Oxy) là k = 0; 0; 1). Đường thẳng d có vectơ chỉ phương là x = (1; 2; 3). Như vậy k, ũ là cặp vectơ chỉ phương của mặt phẳng (P).
Suy ra vectơ n =[k,u]=(2;-1; 0) là vectơ pháp tuyến của (P). Phương trình mặt phẳng (P) có dạng là: 2(x – 2)-(y+3)+0.(2-1)=0 hay 2x – y – 7 = 0.
.. Szzo
Đường thẳng hình chiếu A phải thoả mãn hệ sau: {
(2x-y-7=0. Điểm M(4; 1; 0) A; vectơ chỉ phương ý của đường thẳng A vuông góc với k và vuông góc với n. Vậy, ta lấy ý =[k,n]=(1; 2; 0).
[x = 2+t Phương trình tham số của hình chiếu A có dạng: 4y =−3+2t ,te R.
z=0. b) Tương tự như câu a), mặt phẳng (Oyz) có phương trình x = 0. Lấy điểm M(2; -3; 1) + d và Mg(0; -7; -5) 6 d. .
Hình chiếu vuông góc của MV lên mặt phẳng (Oyz) là điểm M (0; 3; 1) còn hình chiếu vuông góc của Mg lên (Oyz) là chính nó.
| Do đó đường thẳng MM, là hình chiếu vuông góc của đường thẳng d trên (Oyz).
Ta có: MM = (0; 4; -6) || $ =(0; 2; 3). Vậy phương trình hình chiếu của d trên (Oyz) có dạng là:
x=0 y=-3+2t, teR.
z=1+3t Bài 3 (Trang 90, SGK)
- a) Đường thẳng d đi qua M(-3; -2; 6) và có vectơ chỉ phương u =(2; 3; 4). Đường thẳng d đi qua M (5; -1; 20) và có vectơ chỉ phương x = (1;-4; 1).
(1)
Ta có: [u,u,l= (19; 2; -11); MM,18; 1; 14) =[u ,u, JMM, =19.8+ 2.1-11.14 =0. Do đó d và d cắt nhau. Nhận xét: Ta nhận thấy ủ và u, không cùng phương nên d và do chỉ có thể chéo nhau
1-3+2t = 5+ť hoặc cắt nhau. Xét hệ phương trình: -2+3t =-1-4t .
16+41 = 20+t’.
(3) Từ (1) và (3), trừ vế với vế ta có: 2t = 6 + t = 3. Thay vào (2) ta được t = -2. Suy ra d và do có điểm chung duy nhất M(3; 7; 18). Do đó hai đường thẳng d và d cắt nhau.
- b) Đường thẳng d có vectơ chỉ phương 4= (1; 1; -1). Đường thẳng d có vectơ chỉ phương 4 = (2 ; 2; -2) = 2.(1; 1; -1). Vì a = 2.4 =ã và đo là hai vectơ cùng phương.
Mặt khác đường thẳng d đi qua điểm M(1; 2; 3) hay M 6 d. Thế toạ độ của M vào phương trình tham số của đường thẳng d ta có hệ sau:
(1=1+2t (*)/2=-1+2t (2)
13=2–2ť (3) Xét (1) ta thấy t = 0. Giá trị t = 0 không thoả mãn các phương trình (2) và (3). Do đó hệ phương trình (*) vô nghiệm. Suy ra toạ độ của điểm M không thoả mãn phương trình đường thẳng d’ hay điểm M không thuộc đường thẳng d’.
a’ = 2.7 Ta có:
Med, M€ d’ Như vậy d và do song song với nhau. Bài 4 (Trang 90, SGK)
(1+at = 1–ť (1) Để d và d cắt nhau thì hệ (*) {t=2+2t (2) chỉ có một nghiệm
1-1+2+ = 3-t (3) duy nhất.
Như vậy bài toán đưa về việc xác định giá trị a để hệ (*) chỉ có một nghiệm duy nhất.
Xét hệ gồm hai phương trình (2) và (3): {
ft=2+2ť 9:1-1+2t = 3-t’
-2t =-4-4t’
1-1+2t=3-
3-1=-1-5t’
t=0
Với t = 0 thì t = 2.
Để hệ (*) có nghiệm thì các giá trị t = 0 và t = 2 phải nghiệm đúng với phương trình (1), ta có:
1.+ a.2 = 1-0 Aa=0. Vậy với a = 0 thì hệ (*) có một nghiệm duy nhất và khi đó thì d cắt d.
Chú ý: Các giá trị t và t tìm được trên đây là các giá trị của tham số ứng với giao điểm của hai đường thẳng d và d. Bài 5(Trang 90, SGK)
- a) Cách 1:
Thay các toạ độ x, y, z trong phương trình tham số của d vào phương trình (2) ta có:
3(12+4t) +5(9+3t)-(1+t)-2=0 26t+ 78 = 0 t=-3. Khi đó do(a) = M(0; 0; -2).
Trong trường hợp này đường thẳng d cắt mặt phẳng (a) tại một điểm M(0; 0; -2) duy nhất. Cách 2:
ẳng d có vectơ chỉ phương a =(4; 3; 1). Mặt phẳng (a) có vectơ pháp tuyến i=(3; 5; -1).
Xét thấy an = 4.3+3.5+1.(-1) = 26+0. Vây d không song song với (a) nên d cắt (a) tại một điểm duy nhất. b) Cách 1:
Thay toạ độ x, y, z trong phương trình tham số của d vào phương trình (0) ta có:
(1+t)+3(2-t)+(1+2t)+1=0 + 0.t + 9 = 0 + 9 = 0 (vô nghiệm). Chứng tỏ d và (a) không cắt nhau hay d // (a). Cách 2:
Đường thẳng d đi qua điểm M(1; 2; 1) và có vectơ chỉ phương 4 = (1; -1; 2). Mặt phẳng (a) có vectơ pháp tuyến n = (1; 3; 1).
Đườn
Ta có: an = 1 – 3 + 2 = 0. Mà M ¢ (a).
Từ đó suy ra dll (a) hay là đường thẳng d và mặt phẳng (a) không có điểm chung. + c) Cách 1:
| Thay toạ độ x, y, z trong phương trình tham số của d vào phương trình (3) ta có:
(1 + r) +(1+2t)+(2-3t)–4=0
= 0.t + 0 = 0 (phương trình này có vô số nghiệm). Vậy d nằm trên (a) hay d và (a) có vô số điểm chung. Cách 2:
Đường thẳng d đi qua điểm N(1; 1; 2) và có vectơ chỉ phương 4 = (1; 2; -3). Mặt phẳng (d) có vectơ pháp tuyến i = (1; 1; 1).
Ta có ai = 1 + 2 – 3 = 0. Mà Ns (a). | Từ đó suy ra đường thẳng d nằm trong mặt phẳng (a) hay d và (a) có vô số điểm chung. Bài 6 (Trang 90, SGK)
Thay toạ độ x, y, z trong phương trình tham số của A vào phương trình mặt phẳng (d) ta có:
2(-3 + 2t) – 2(-1 + 3t) + (-1 + 2t) + 3 = 0
= 0.t = 2 (phương trình vô nghiệm). | Do đó đường thẳng A song song với mặt phẳng (d). Như vậy khoảng cách giữa A và (a) bằng khoảng cách từ một điểm M(3; -1; -1) thuộc A đến mặt phẳng (d).
Ta có: d(A, (x)) = d(M, (0)). Áp dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng, ta có: almol_12.(-3) – 2.(-1)-1+3_1-6+2-1+3] 2
V2+(-2) +12 Bài 7 (Trang 91, SGK)
- a) Đường thẳng A có vectơ chỉ phương 4= (1; 2; 1).
| Điểm H thuộc đường thẳng A nên toạ độ của H phải thoả mãn phương trình A, hay toạ độ của H là (2+t; 1+2t;t).
3 AH =(1+t; 1+2t;t).
Để H là hình chiếu vuông góc của A trên A thì AH Lã hay AHã= 0. = (1+t).1+(1+2t).2+t.1=0
6t+3=0 at
Thay giá trị t=-2 vào phương trình tham số của A ta có:
3
y=1+2(+1)= v= = (: 0: -)
y=1+2.
0
H
–
7
=
–
– 2
Z
=:
—
- b) Gọi A là điểm đối xứng của A qua A.
= AA’ = 2AH = {ya:-0=2.(0-0) {y^- = 0)
Như vậy ta có điểm A(2; 0; -1). Bài 8 (Trang 91, SGK)
- a) Gọi A là đường thẳng đi qua M và vuông góc với mặt phẳng (a), vectơ pháp tuyến n = a = (1; 1; 1) là vectơ chỉ phương của A nên A có phương trình tham số là:
x =:1+t y = 4+t Z=2+t
Toạ độ H là nghiệm của hệ phương trình:
x =1+t y = 4+t z=2+
(3)
(x + y +2-1=0
Thay (1), (2), (3) vào (4) ta có: 1+t+4+t+2+t-1=0 – 3t+6=0 @t=-2.
Khi đó thì x = -1; y = -2; z = 0. Vậy H(-1; 2; 0). . b) Gọi M(x, y, z) là điểm đối xứng của M qua mặt phẳng (a), thì hình chiếu vuông góc H của M xuống mặt phẳng (d) chính là trung điểm của MM. Ta có: X+1
– -14X =-3; . =2 Hy=0; = Z=-2. 2 Vậy M (-3; 0; 2). c) Tính khoảng cách từ M đến mặt phẳng (3) bằng hai cách sau: Cách 1:
1+ 4+2 -1 Áp dụng công thức ta có: dọM, (())==
y +4
X=-3.
lu:
VI+1+1″
=213.
Cách 2: Khoảng cách từ M đến mặt phẳng (3) chính là khoảng cách MH:
d(M, (a)) = MH = V22 +22 +22 = 213. Bài 9 (Trang 91, SGK)
Đường thẳng d đi qua điểm M(1; 2; 0) và có vectơ chỉ phương (-1; 2; 3). Đường thẳng d đi qua điểm M(1; 3; 1) và có vectơ chỉ phương (1;-2; 0). Cách 1:
Ta có [..] ( 3, 4 | 2 = (2,1-5), MM =(0,1)
Mà [u, u’MM = 2.0+1.1+(-5).1= -4 + 0.
Do đó d và do chéo nhau. Cách 2:
Vì ủ và u không cùng phương nên d và d chỉ có thể là chéo nhau hoặc cắt nhau.
Ta xét số giao điểm của d và do: (1-1=1+t (t+t’ =0) {2+ 2+ = 3– 2 = 2t+2 =1 (hệ vô nghiệm). 3t = 1
|3t = 1 Do đó d và do không thể cắt nhau. Vì vậy d và do chéo nhau. Bài 10 (Trang 91, SGK)
Ta chọn hệ toạ độ Oxyz sao cho 0= A, i=AB, j=AD, k = AA Trong hệ toạ độ Oxyz ta có: A'(0:0;1), B(1; 0; 0), D(0; 1; 0), B’ (1; 0; 1), D'(0; 1; 1), C(1; 1; 0).
Đặt (x) = (ABD) và (B) = (BDC), ta có phương trình của các mặt phẳng (a), (B) là:
x ): –+
y
z
+
–
1
Be
DX + y +z-1=0 (B): (x –1)+(y-1) +z = 0
X — y +2 – 2 = 0. Vì A(0; 0; 0) nên suy ra: d(A, (q))=-111_ V3.
V1? +1+12
1-2
d(A,(B))=
-2/3
V1° +1° +12


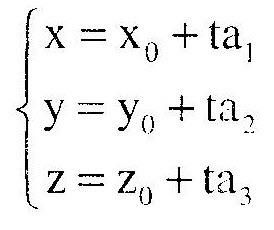 trong đó t là tham số.
trong đó t là tham số.

 đến mặt phẳng (α):
đến mặt phẳng (α):