Bài 1 (Trang 26, SGK)

Các đỉnh, cạnh, mặt của một đa diện phải thoả mãn hai tính chất sau:

– Hai mặt phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.

– Mỗi cạnh của mỗi mặt nào cũng là cạnh chung của đúng hai mặt. Bài 2 (Trang 26, SGK)

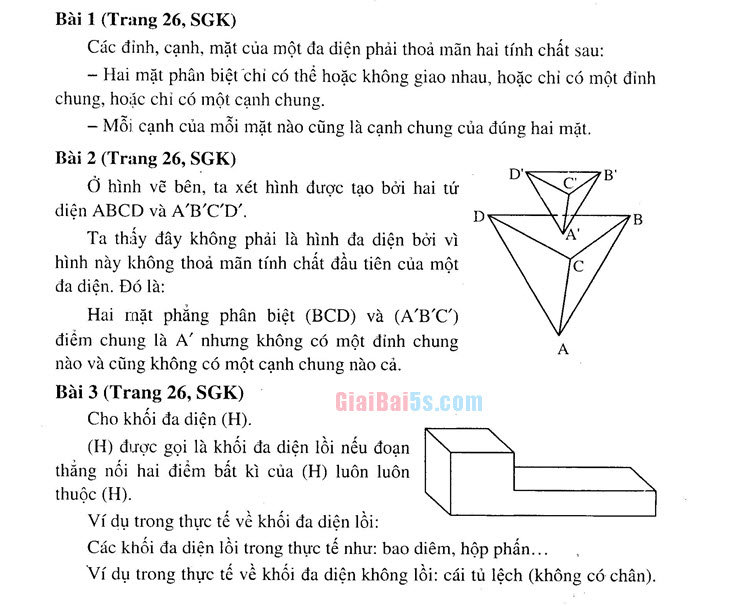
D’OB Ở hình vẽ bên, ta xét hình được tạo bởi hai tứ diện ABCD và A’B’C’D.

Ta thấy đây không phải là hình đa diện bởi vì hình này không thoả mãn tính chất đầu tiên của một đa diện. Đó là:

Hai mặt phẳng phân biệt (BCD) và (ABC) điểm chung là A’ nhưng không có một định chung nào và cũng không có một cạnh chung nào cả. Bài 3 (Trang 26, SGK)

Cho khối đa diện (H).

(H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn luôn thuộc (H).

Ví dụ trong thực tế về khối đa diện lồi: Các khối đa diện lồi trong thực tế như: bao diêm, hộp phấn… Ví dụ trong thực tế về khối đa diện không lồi: cái tủ lệch (không có chân).

Bài 4 (Trang 26, SGK)

Gọi V1, V2 lần lượt là thể tích của khối lăng trụ và khối chóp. Gọi S, h lần lượt là diện tích đáy và chiều cao của cả khối lăng trụ và khối chóp. Theo công thức ta có: v, =Sh và V, =sh.

Từ đó suy ra :

on

= 3.

4. V. 1S.h

Vậy tỉ số thể tích giữa khối lăng trụ và khối chóp có cùng diện tích đáy và chiều cao là 3. Bài 5 (Trang 26, SGK)

Gọi E là chân đường vuông góc hạ từ C xuống AB. H là chân đường vuông góc hạ từ O xuống CE.

ViOA LOC “lOB nên OCE(OAB).

тн

=OC LAB và OC IOE. Ma SABICE AB 10C

– nên AB (OEC). >ABLOH,AB 1 OE. (OH I AB OH ICE

P=OH 1 (ABC). Tam giác OAB vuông tại 0 (vì theo giá thiết OAI OB). OE là đường cao ứng với cạnh huyền AB nên ta có:

1 1 1 1 1 OE OAP * OBa? 62 Tam giác OCE vuông tại O. OH là đường cao ứng với cạnh huyền CE. Suy ra: OH? OE2 * Oc? a? +62 1 a?b? + b2c? +cʻa?

Va’b? +be? +ca? Nhận xét: Ta có thể tính độ dài đoạn OH từ mối liên hệ:

abc

OH

OH2=

–

a2b2c2

V.Abc = abc = Sanpc.OH

O.ABC

BOH= 2S ABC

OH – abc

Bài 6 (Trang 26, SGK)

Gọi trung điểm của BC là E.

Kẻ SHI. (ABC). Khi đó H chính là trọng tâm của tam giác đều ABC. Do đó H thuộc AE, suy ra:

2

AH ==AE

(1)

AE là trung tuyến của tam giác đều ABC nên AE AE I BC. Tam giác ABE vuông tại E nên ta có:

H

AE = AB.sin 60o =

(2)

B

1. AHav3

Từ (1) và (2) suy ra: AH =

3 H là hình chiếu của S trên mp(ABC). Suy ra HA là hình chiếu của SA trên mp(ABC). Hay là góc giữa SA và mp(ABC) là SAH và bằng 60.

SHI (ABC) nên tam giác SAH vuông tại H. Do đó ta có:

SH = AH.tanSAH =

av

SH = AHtanSAH = a ¥3. tan60° – ay3.13=a.

utan

3

Vì SH I (BCD) nên SA IDE. Tam giác ADE vuông tại D nên

DE = AE sindAE = ay3 sing0o = 4y3 13 = Va DA = AE.cos DAE = ax 3 cos 60° – ap?

SH Tam giác SAH vuông tại H nên SA =>

sinSAH

Ta có: SD+DA=SA

SD=SA-DA==

3

4

1. a) Áp dụng công thức tính tỉ số thể tích trong Bài 4 (Trang 26, SGK), ta có tỉ số thể tích của hai khối chóp S.DBC và S.ABC là:

Vs.DBC_SD SB SC _SD_.513 213_5

Vsap SA SB SC SA 12 398 b) Ta có:

S.DBO

S.ABC

Scre = 4*23; SH=a.

AABC

=> Vs ABC = 1 a? V3 = a03

S.ABC

4.

Từ đó suy ra vụ bac = x –

3

S.DBC

S.ABC

8

96

Cách khác:

Sape = L.DE.BC = Ba2

ADBC

.

Vs.DBC = Sabsc-SD = a°513

S.DBC

96

A

Bài 7 (Trang 26, SGK)

Gọi H là chân đường vuông góc hạ từ S . xuống mp(ABC). Từ H kẻ HEL AB, HFIBC, HJ 1 AC.

Vì SEH, SFH và SSH đều bằng 60 nên HE = HF = HJ = r là bán kính đường tròn nội tiếp tam giác ABC.

Nủa chu vi tam giác ABC bằng p = 9a. Áp dụng công thức Hê-rông ta tính được diện tích tam giác ABC là: S= 1p(p-a)(p-b)(p-c) = 19.4.3.2.a’ = 6/6.a?.

S 6V6.a? 26.a Áp dụng công thức S =p.r, ta có:r ====

р 9а Xét tam giác vuông SEH ta có:

SH = HE. tan 60o =rV3. = 216.a. 13 = 2/2a. Vậy Vs Are SHS Jurc = -2722.676.a?=8/3a”.

S.ABC

Bài 8 (Trang 26, SGK)

(BC1 BA Ta có: 4 = BCL (SAB).

BCISA Mà AB =(SAB) nên BCI AB. (1) Mặt khác ABISB.

(2) Từ (1) và (2) suy ra AB (SBC) Do đó ABISC. Chứng minh tương tự ta có AD SC. (AB’ISC

NB’

AD’ISC-SC 1(AB’D’).

Ta có SB = a +c); SD= b + c và SC = a + b +c. Sử dụng phương pháp tính diện tích ta có: SA.AB = AB’SB > AB’ = SA.AB – _ ac

SB Vate? Chứng minh tương tự ta có:

bc

AD’=beş: ACP = cova’ + b

Vb+ca

Va’ + b + c

Từ đó suy ra:

I

Chứng minh tương tự ta có:

$8′ = VSA’– ABP = your $D’ = vo teises voit hotel Vì hai tam giác SCB và SBC đồng dạng nên BCC

B’C’

BC SB

SC

Từ đó suy ra: pipe_ BC.SC’ b.c? B’C’ =–

– SB Ja2 + b2 + c2 sa2tc2 Chứng minh tương tự ta có:

a.c?

DC = T2b2 te shte

Vì ABI BC và ADIDC nên:

1

c2

ac

Save ={8C?AB = 2 vas te vertete volte

S.

AB’C’

B

2 Va? +c? Va? + b2 +c2 Va? +c

abc?

2° (a’ +c?).Va’+b+c?

Chứng minh tương tự ta có S.ABC ==

abc

2).Va’ + b2 +c?

Vậy thể tích của hình chóp phải tìm là:

11

abc3

/

* chóp

dola

3 2

la2 +t

2+0211221

a? + b2 + c2

1 abco _ a’+b? +2c?___ abco (a’ + b2 +2c=)

6°a? +b+c’ (a’ +c?)(b’+c?) 6(a’ +c?)(b? +c?)(a’ + b2 +ca) Bài 9 (Trang 26, SGK)

Gọi giao điểm của AC và BD là 0. AM cắt SO tại I. Dễ thấy EF qua I và song song với BD. Ta có: (BCI AC (theo giá thiết)

BDISO (vì S.ABCD là hình chóp đều) BDI(SAC)

Theo trên EF // BD nên EF I (SAC). Từ đó suy ra EFI SC

(1) Mặt khác tam giác SAC cân tại S, hơn nữa theo giả thiết thì góc giữa SA và mp(ABCD) bằng 60°, tức là SAC = 60° nên suy ra tam giác SAC là tam giác đều. Vì M là trung điểm của SC nên AMISC.

(2) Từ (1) và (2) suy ra SCI (AEMF). Do đó SM là chiều cao của khối chóp S.AEMF. SEF I (SAC)

nên EFI AM. AMC (SAC)

(2)

A

AEMF

S.AEMF

SAEME = -EF.AM. VS AEME = – EF.AM.SM ABCD là hình vuông cạnh a nên đường chéo AC có độ dài bằng a/2. Tam giác SAC là tam giác đều, AC = a/2 nên SC=a/2. Vì M là trung điểm của SC nên SM = 4×4

Mặt khác tam giác SAC đều, AC = a/2 nên đường cao AM = AC.sin60° = avo

(4) Dễ thấy I là trọng tâm của tam giác SBD nên theo định lí Ta-lét ta có:

EF = SI – – EF = {BD = 2/22

3

BD SO 37 Thay thế (3), (4), (5) vào (*) ta có:

1 2VZa ato av2 _ a’ J6 (dvtt).

S.AEMA

“S.AEM= 6 3 2 2 18 Bài 10 (Trang 27, SGK)

1. a) Ta tính thể tích tứ diện ABCB hay là thể tích hình chóp A .BCB như sau:

Gọi M là trung điểm của BC, ta có: AMI. B’C’

(1) Lăng trụ ABC.ABC là lăng trụ đứng nên ta có:

BB’ 1. (A’B’C’) Mà A Mc(A’B’C’) nên BB1 AM (2)

Từ (1) và (2) suy ra AoMi (BBC) hay AM là đường cao của hình chóp A’. BCB’.

Tam giác ABC là tam giác đều cạnh a, AM là đường cao nên

Α

A’M = a.sin 60o =

BBC là tam giác vuông cân tại B nên SBBC = a^.

> Vnes = AM.

Sc = 1 a 3 ha?

ABCB’

B’

a 13 (dvtt).

I

ABCI

man

M

= VABCB =

12 b) Thể tích hình chóp C.A’B’FE bằng tổng thể tích hai hình chóp:

– V, là thể tích hình chóp đỉnh B, đáy là tam giác CEF.

– Vì là thể tích hình chóp đỉnh B, đáy là As ta n giác ABC.

Vì mp(ABC) song song với mp(ABC) nên ta có EF // AB, Lại có:

EF=a. Hình chóp BCEF có chiều cao BB’ = a và diện tích đáy là:

VA

C

Suy ra v

1 2 Vì EC=>AC nên Sen = -.-a.a =

A’EC

23 3 Hình chóp B’.AEC có chiều cao là BI (chiều cao của AA’B’C).

B1=42= v. =

18

–

+–

Vậy thể tích hình chóp C.A’B’FE là:

a 13 až 13 5 13a3 V = V, + V, =

(đvtt). * 27 1854 Bài 11 (Trang 27, SGK)

| Đầu tiên, ta xác định thiết diện của hình hộp ABCD.A’B’C’D khi cắt bởi mp(CEF).

Mặt phẳng (CEF) chứa đường thẳng EF mà E là trung điểm của BB’, F là

trung điểm của CC nên EF chúa giao điểm 0 của các đường chéo hình hộp. Do đó mặt phẳng (CEF) cùng chứa giao điểm O của các đường chéo và nó cũng chứa đường chéo AC của hình hộp.

Ta có thể nhận thấy rằng thiết diện cần tìm chính là hình bình hành CEAF.

Qua EF ta dựng một mặt phẳng song song với | đáy hình hộp, mặt phẳng này cắt AA’ ở P và cắt CC A.

ZE

ở Q.

1

ABCD.PEQF

ABCD.A’B’C’p’

CFOF

A’PEF

Thể tích của hình hộp ABCD.PEQF là:

Vaderd Peep = = VABCD.ABC’O (1) Ta cũng chứng minh một cách dễ dàng rằng:

VcFQE = VAPep (2) (Vì hai hình chóp CFQE và A PEF có chiều cao bằng nhau và diện tích đáy bằng nhau.)

Xét khối đa diện ABCDEAF do mặt phẳng (CEF) chia ra trên hình hộp ABCD.A’B’C’D, ta có như sau:

VABCD.FA_EQ = VABCD.IPE + VA PEF Từ (1), (2) và (3) suy ra: VABCD.Fate = — VABCD.ABCD”

Như vậy mặt phẳng (CEF) chia hình hộp thành hai khối đa diện có thể tích bằng nhau và tỉ số giữa chúng bằng 1.

Chú ý:

Còn có thể lí luận như sau: Giao điểm O của các đường chéo hình hộp là tâm đối xứng của hình hộp. Do đó, mặt phẳng (CEF) chúa điểm 0 nên chia hình hộp thành hai hình đối xứng với nhau qua điểm O.

| Do đó hai hình này là hai hình bằng nhau cho nên chúng có thể tích bằng nhau. Như vậy tỉ số thể tích giữa chúng bằng 1. Bài 12 (Trang 27, SGK)

| a) Xét khối tứ diện (khối chóp) M.AND. Chiều có của khối chóp này (hạ từ đỉnh Mì chính bằng độ dài cạnh AA của hình lập phương.

Do đó: YMAND = AA’S AND

ABCD.FA’EO

ABCD.A’B’C’D’:

AA’ = a. Ssand = SABCD = SACND – SAABN

= a_a__a’_a?

Ā

Ā=

(3)

a 3

1 3

a 2 2

M.AND

6

Thay thế (2) và (3) vào (1) ta có: VM.AND = … Vậy thể tích khối tứ diện ADMN là 2 (đvt). b) Chia (H) thành các hình chóp FDBN, D.ABFMA’ và D.A EM. Dễ thấy FN || ED, nên hai tam giác FBN và DDE đồng dạng. Từ đó suy r

vra

BN ED” 3′ do do BF = 3a;

1 a? 2a ay SDBN =

đó VFDBN = =.=.===

3.4.3

PDRM Sa?

FMB

-..

ABFMA’

= Sxermax = 11a Do đó V, Aura 3g 4 – 8

1 lla? -,- .a

1 la

Do đó VD.ABFMA

=

3 12

1 a a Same =-.-.-

23

1 a?

a —

an

Sa’me=774 16

do đ

A

3 16

16

a?

Suy ra Vous =

+

11a3 36

Suy ra Vy =

?

o

+

a3 48

55a3 144

isa

18

V1H1) = a – 55a’ 89a

(H) = a +144 = 144 VH) _55a89a55 Von 144144 89