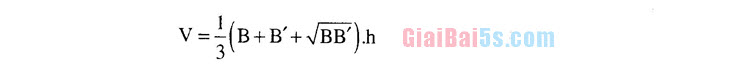| A. KIẾN THỨC CƠ BẢN
1. Khái niệm Có thể đặt tương ứng cho mỗi khối đa diện (H) một số dương duy nhất VH) thoả mãn các tính chất như sau: – Nếu (H) là khối lập phương cạnh bằng 1 thì V(H) = 1. – Nếu hai khối đa diện (H1) và (H2) bằng nhau thì V(H1) = V(H2) – Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H2) thì: V(H) -V(H1) +V(H2). Số dương V(H) nói trên được gọi là thể tích của khối đa diện (H). Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị. Nếu (H) là khối lăng trụ ABC.A’B’C’ thì thể tích của nó được kí hiệu là: V(ABC.A’B’C’) 2. Các định lí – Định lí 1: Thể tích của một khối hộp chữ nhật bằng tích số ba kích thước của nó. – Định lí 2: Thể tích của khối lăng trụ có diện tích đáy B và có chiều cao h là: V= B.h – Định lí 3: Thể tích của khối chóp có diện tích đáy B và có chiều cao h là:
Thể tích của khối chóp cụt có diện tích hai đáy theo thứ tự là B, B’ và có chiều cao h là:
3. Kiến thức bổ sung – Cho hình chóp S.ABC. Trên ba tia SA, SB, SC lần lượt lấy ba điểm A’, B’, C’. Khi đó, ta có như sau:
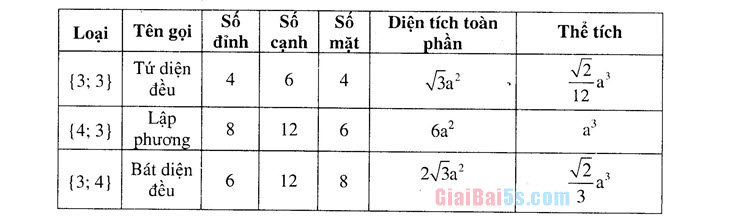
– Bảng tóm tắt của năm loại khối đa diện đều:
Diện tích toàn phần và thể tích được tính theo cạnh a của đa diện đều |




Nguồn website giaibai5s.com
- KIẾN THỨC CƠ BẢN 1. Khái niệm
Có thể đặt tương ứng cho mỗi khối đa diện (H) một số dương duy nhất VH) thoả mãn các tính chất như sau:
– Nếu (H) là khối lập phương cạnh bằng 1 thì VH) = 1. – Nếu hai khối đa diện (H) và (Hạ) bằng nhau thì VH) = VH)
– Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H) thì: VH) -VH, +VH,).
Số dương VH) nói trên được gọi là thể tích của khối đa diện (H).
Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị. Nếu (H) là khối lăng trụ ABC.A’B’C’ thì thể tích của nó được kí hiệu là:
(ABC.A’B’C’)
- Các định lí
– Định lí 1: Thể tích của một khối hộp chữ nhật bằng tích số ba kích thước của nó.
– Định lí 2: Thể tích của khối lăng trụ có diện tích đáy B và có chiều cao h là:
V= B.h – Định lí 3: Thể tích của khối chóp có diện tích đáy B và có chiều cao h là:
V=Bh Thể tích của khối chóp cụt có diện tích hai đáy theo thứ tự là B, B’ và có chiều cao h là:
V=(B+B + VBB“).
- Kiến thức bổ sung
– Cho hình chóp S.ABC. Trên ba tia SA, SB, SC lần lượt lấy ba điểm A, B’, C’. Khi đó, ta có như sau:
VSABC – SA’ SB’SC
VS.ABC SA ‘SB SC – Nếu (H) là ảnh của (H) qua một phép dời hình thì: VH) =VH). Nếu (H) là ảnh của (H) qua một phép vị tự tỉ số k thì: VR =k^.VH). – Bảng tóm tắt của năm loại khối đa diện đều:
Số 1 Số 1 Số 1 Diện tích toàn Loai | Tên gọi | đỉnh | cạnh | mặt 1
Thể tích Tứ diện
V3a
(H)
phần
{3; 3}|
đều Lập
{4;3}
| 12 | 6
622
نرم
| 8 phương Bát diện
6
2/3a?
{3; 4}
đều
13(3+V5) a?
Số 1 Số 1 Số 1 Diện tích toàn Loại 1 Tên gọi
Thể tích đỉnh | cạnh 1 mặt
phần Mười {5; 3} | hai mặt | 20 | 30 | 12 | 3/25 +10/5a (15+7/5)a
đều
Hai {3; 5} } mươi | 12 | 30 mươi
513a?
20 mặt đều Diện tích toàn phần và thể tích được tính theo cạnh a của đa diện đều. B. HƯỚNG DẪN GIẢI BÀI TẬP (SGK) Bài 1 (Trang 25, SGK)
| Tứ diện đều ABCD cũng là hình chóp đều ABCD với các cạnh bằng nhau và bằng a. Gọi H là chân đường cao kẻ từ A xuống mặt phẳng đáy (BCD). Khi đó H là tâm đường tròn ngoại tiếp tam giác đều BCD.
Kẻ AH cắt CD tại M. Khi đó M là trung điểm CD và BMICD.
BM là đường cao của tam giác đều BCD, suy ra:
BM == BC.sin BCM = a.sin 60o =
BH = {BM= BH = 473
3
Tam giác ABH vuông tại H, áp dụng định lí Pi-ta-go ta có: AB = AH+ BH?
AH = AB- BH
– A#°=a? =(, 3) => AH – YOU BCD là tam giác đều cạnh a nên ta có Sacp = 3a. sv1 Vaa V3a? _V2a
CD –
>> YABCD = 33.-12
CD
Bài 2 (Trang 25, SGK)
Cho khối bát điện đều ABCDEF cạnh a. Do AE = AF=BE = BF = CE = CF = DE = DF nên bốn điểm A, B, C, D cùng nằm trên mặt phăng trung trực của đoạn thẳng EF. Mặt khác ta có AB = BC = CD = DA nên tứ giác ABCD là hình thoi.
AG Vì EA = EB, OE là cạnh chung nên AEOA = AEOB. Suy ra OA = OB.
= AC = BD. Hình thoi ABCD có hai đường chéo bằng nhau nên ABCD là hình vuông.
Từ đó suy ra thể tích hình tam cạnh đều E.ABCD.F bằng tổng thể tích của hai hình chóp tứ giác đều E.ABCD và F.ABCD hay là bằng hai lần thể tích hình chóp tứ giác đều E.ABCD.
- ABCD.F = 2. VE.ABCD Tam giác OAE vuông tại O, áp dụng định lí Pi-ta-go ta có: AE? = OE?+OA? + OE? = AE? – OA’=a? 22% – 23% –
- 2 = 0E = 42 => VEABCD = .0ES,2cm = ay? a? – v2.
Váy Ve xuros de Bài 3 (Trang 25, SGK)
| Gọi S là diện tích đáy ABCD và h là chiều cao của khối hộp. Ta chia khối hộp thành khối tứ diện ACBD và bốn khối chóp A.ABD, c.CBD, B.BAC và D.DAC.
Ta có diện tích tam giác ABD là: Sapo = Satco = -s. Do đó thể tích khối chóp A.ABD là:
E.ABCD
ABCD
3
2
E.ABCD.F
ABD’
CL
*
*
V ABD
-.h.-S=-S.h
A’
C’B’D’
B’.BAC
D’.DAC
Chứng minh tương tự ta có: Vccopy = Veg:BAC = Vo:DAC = -s.h Vậy thể tích khối tứ diện ACBD là: VxCBD = VABCD.ABCD) – 4.VA.ABP = S.h – 4s.h = -s.h Vậy Vaco AWC Sh = 3. vas VACB’D’ S.h
ACB’D’
ABCD.A’B’C’
AA’B’
ABCD.A’B’C’D’
ACB’D’
SAB
HA
VSA
Bài 4 (Trang 25, SGK) | Gọi ASB là a. Khi đó ta có: SsaB = -SA.SB.sina (1)
Akt—tar Ssap = -SAʼSB”sina (2)
Gọi H và H lần lượt là hình chiếu của C và C trên mặt phẳng (SAB). Khi đó hai điểm H và H cùng nằm trên giao tuyến giữa mp(SAB) và mặt phẳng vuông góc với mp(SAB) và chứa SC. Suy ra HC || HC.
Xét tam giác SHC có He SH, Ce SC và HC / HC. Suy ra ASHC và ASHC là hai tam giác đồng dạng.
H’C’ SC
HC-SC
(3)
(5)
V
Mặt khác ta lại có: VGABC =SSAB.HC. (4) Vs.ABC = SsAp.HC. Từ (1), (2), (3), (4) và (5) suy ra:
A.SB’.sin a.H’C’. VSABC – ZSsapHC
SA’ SB’SC SA.SB.sina.HC
SA SB SC Đó là điều phải chứng minh. Bài 5 (Trang 26, SGK) “Ta có: (AB 1. CD
AB I (ACD) AB I. AC
Vs ABC
S.ABC
SAB
.HC
Mà CE C (ACD) > AB I CE (1) Mặt khác có BDI (CEF)= BDICE (2) Từ (1) và (2) suy ra CE (ABD). =CE I EF, CE I AD.
Vì tam giác ACD vuông cân tại C, CA = CD = a. Áp dụng định lí Pi-ta-go ta tính cá được AD = a 2. CE là đường cao ứng với cạnh huyền AD nên CE cũng đồng thời là đường trung tuyến.
CE = L AD = ay? Ta có: BC = a2, BD = 2a + a = a/3.
Mà CEBD = DC BC nên CF-4 v2 = 12
av353
Tam giác CEF vuông tại E nên áp dụng định lí Pi-ta-go ta có:
2a? CF? = EF+CE?
a? a? EF? = CFP – CEP =
3 2
6
Tam giác DCF vuông tại F nên áp dụng định lí Pi-ta-go ta có: DC = CF? + DF? = DF? = DC- CF* = a -21
DF = av? Do đó. Sau – EECE – 6 7 8 Vậy Vua – San DF-J – ay 3
DER
D.CEF
Bài 6 (Trang 26, SGK)
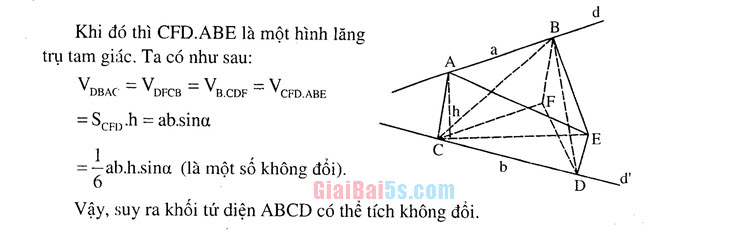
Gọi độ dài đường vuông góc chung giữa hai đường thẳng chéo nhau d và do là h, gc giữa d và do là ct.
Qua ba điểm B, A, C dựng hình bình hành BACF. Qua ba điểm A, C, D dựng hình bình hành ACDE.
| Khi đó thì CFD.ABE là một hình lăng trụ tam giác. Ta có như sau:
VpBac = Vprce = VB.cipe = VCFD.ABE = ScFv)h = ab.sina
ab.h.sina (là một số không đổi). Vậy, suy ra khối tứ diện ABCD có thể tích không đổi.