A. KIẾN THỨC CƠ BẢN 1. Khối đa diện lồi

Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của đa diện (H) luôn thuộc (H). Khi đó, đa diện giới hạn (H) được gọi là đa diện lồi.

Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của đa diện đó. 2. Khối đa diện đều

Định nghĩa: Khối đa diện đều là khối đa diện lồi có các tính chất sau: – Mỗi mặt của nó là một đa giác đều p cạnh.

– Mỗi đỉnh chung của nó là đỉnh chung của đúng q mặt. Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.

– Các mặt của khối đa diện đều là những đa giác đều và bằng nhau. Định lí:

Chỉ có năm loại khối đa diện đều. Đó là các khối đa diện đều loại {3; 3}, loại {4; 3}, loại {3; 4}, loại {5; 3} và loại {3; 5}.

Bảng tóm tắt của năm loại khối đa diện đều: Loại Tên gọi Số đỉnh | Số cạnh

Số mặt {3; 3} | Tứ diện đều {4; 3} Lập phương {3; 4} | Bát diện đều {5; 3} | Mười hai mặt đều {3; 5} | Hai mươi mặt đều

– Hai khối đa diện đều có cùng số mặt thì đồng dạng với nhau.

– Hai khối đa diện đều có cùng số mặt và có cạnh bằng nhau thì bằng nhau. B. HƯỚNG DẪN GIẢI BÀI TẬP (SGK) Bài 1 (Trang 18, SGK)

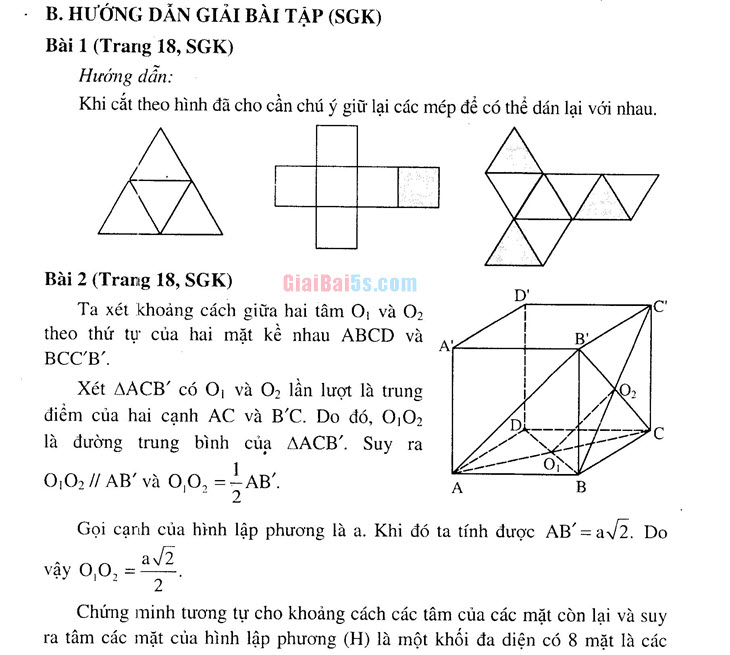
Hướng dẫn: Khi cắt theo hình đã cho cần chú ý giữ lại các mép để có thể dán lại với nhau.

Bài 2 (Trang 18, SGK) | Ta xét khoảng cách giữa hai tâm O và O2 theo thứ tự của hai mặt kề nhau ABCD và BCC’B’. | Xét AACB có O và O, lần lượt là trung điểm của hai cạnh AC và BC. Do đó, OGO là đường trung bình của ACB. Suy ra 0,0, // AB và 00, = AB.

Gọi cạnh của hình lập phương là a. Khi đó ta tính được AB = a/2. Do vậy 0,0, = a 2.

2

Chứng minh tương tự cho khoảng cách các tâm của các mặt còn lại và suy ra tâm các mặt của hình lập phương (H) là một khối đa diện có 8 mặt là các

tam giác đều, có cạnh là a2 Diện tích toàn phần của hình lập phương (H) cạnh a là:

S= 6a? (1)

Diện tích một mặt của bát diện đều (H) cạnh –

ne av

là:

2

Diện tích hình bát diện đều (H) đó là:

Sw) = 8.S = a’ 13. (2)

.

Từ (1) và (2) suy ra: °(H) – 6a

(H)

a? 5 = 2V3.

M

Bài 3 (Trang 18, SGK).

Cho hình tứ diện đều ABCD có cạnh bằng a. Khi đó ABC, ABD, ACD, BCD là các tam giác đều bằng nhau cạnh a.

Gọi E, F, I, J lần lượt là trọng tâm của các mặt ABC, ABD, ACD, BCD. Gọi M là trung B điểm của AB. ME MF 1

suy ra EF // CD. MC MD

Ta có: !

win wl

– Do đó: EF

Chứng minh tương tự, ta có các cạnh khác của tứ diện EFIJ đều bằng 4.

Do đó, tứ diện EFIJ là một tứ diện đều. Bài 4 (Trang 18, SGK)

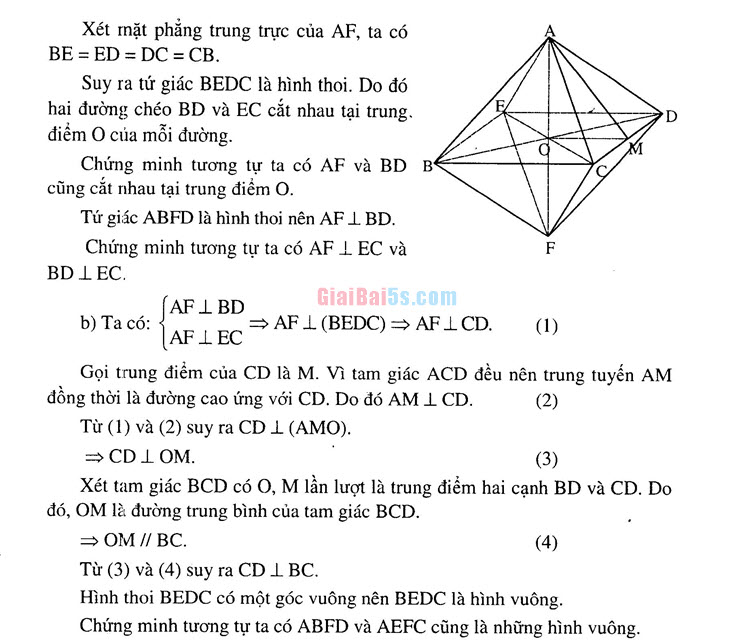
1. a) Ta có: EA = EF, CA = CF, BA = BF, DA =DF. Suy ra bốn điểm B, C, D, E cùng nằm trong mặt phẳng trung trực của AF.

Xét mặt phẳng trung trực của AF, ta có BE = ED = DC = CB.

Suy ra tứ giác BEDC là hình thoi. Do đó hai đường chéo BD và EC cắt nhau tại trung. điểm 0 của mỗi đường.

| Chứng minh tương tự ta có AF và BD Bé cũng cắt nhau tại trung điểm O. | Tứ giác ABFD là hình thoi nên AF1BD.

Chứng minh tương tự ta có AFI EC và BDI EC.

(AFI BD b) Ta có: 2 = AFI (BEDC)=AFLCD.

(1)

(AF I EC

(3)

Gọi trung điểm của CD là M. Vì tam giác ACD đều nên trung tuyến AM đồng thời là đường cao ứng với CD. Do đó AM ICD. (2)

Từ (1) và (2) suy ra CD (AMO).

→ CD I OM.

Xét tam giác BCD có 0, M lần lượt là trung điểm hai cạnh BD và CD. Do đó, OM là đường trung bình của tam giác BCD. BOM / BC.

(4) Từ (3) và (4) suy ra CD l BC. Hình thoi BEDC có một góc vuông nên BEDC là hình vuông. Chứng minh tương tự ta có ABFD và AEFC cũng là những hình vuông.