1. Thế nào là phần thực, phần ảo, môđun của một số phức? Viết công thức tính môđun của một số phức theo phần thực và phần ảo của nó.

Giải | Mỗi số phức là một biểu thức z = a + bị với a,

. – у be R, 12 = -1 – Số thực a là phần thực của số phức:

z = a + bi – Số thực b là phần do của Số phức z = a + bị

– Điểm M(a; b) trên mặt phẳng tọa độ biểu diễn số phức z = a + bi

Khi đó độ dài vectơ OM gọi là môđun của z, kí hiệu z =OM Ta có công thức a + b) = a +b^.

| 2. Tìm mối liên hệ giữa khái niệm môđun và khái niệm giá trị tuyệt . đối của loột số thực

Giải : Mỗi số thực a được coi là một số phức có phần ảo bằng 0 Ta có: a + R = a = a + 0i Môđun của số thực a là:

1a + 0i1 = Va? +0? = [a] Như vậy với một số thực, khái niệm môđun và khái niệm giá trị tuyệt đối là đồng nhất. . . . 3. Nêu định nghĩa số phức liên hợp với số phức z. Số phức nào bằng , số phức liên hợp của nó? .

Giải Cho số phức z = a + b) (a, b + R) thì số phức liên hợp của số phức z kí hiệu là:

z = a – bi. Số phức z bằng số phức liên hợp của nó z khi và chỉ khi z là số thực.

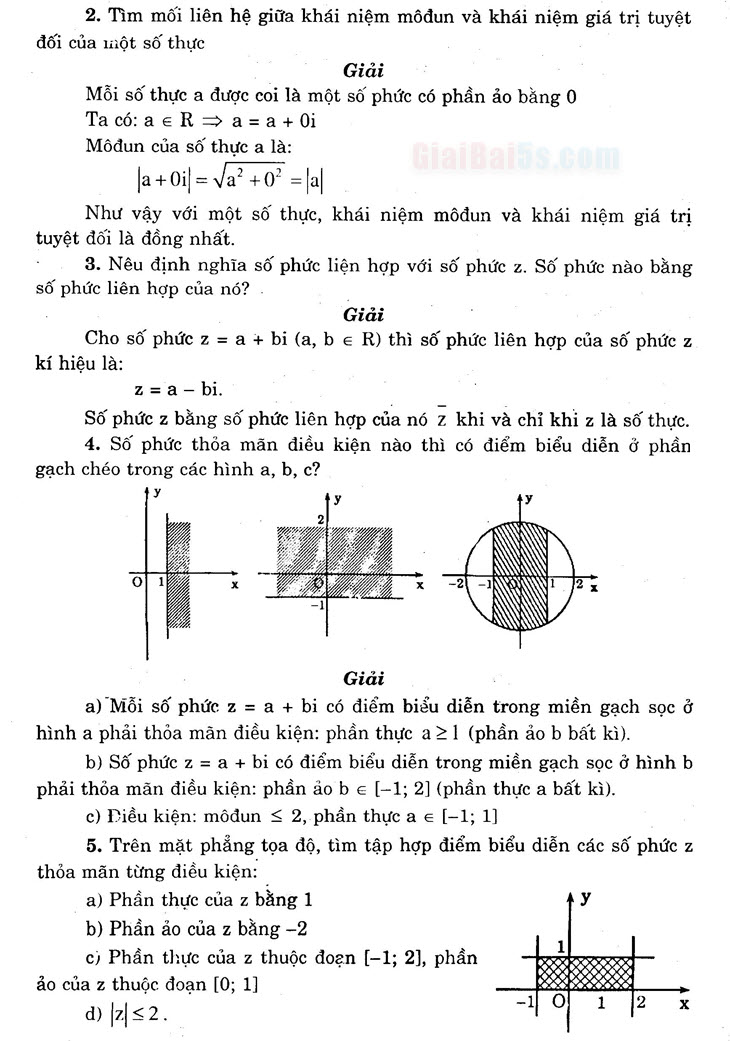
4. Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình a, b, c?

.

:

..

o

X

Giải a) Mỗi số phức z = a + bị có điểm biểu diễn trong miền gạch sọc ở hình a phải thỏa mãn điều kiện: phần thực a>1 (phần ảo b bất kì).

1. b) Số phức z = a + bị có điểm biểu diễn trong miền gạch sọc ở hình b phải thỏa mãn điều kiện: phần ảo b c [-1; 2] (phần thực a bất kì).
2. c) Điều kiện: môđun < 2, phần thực a + (-1; 1]
3. Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện:
4. a) Phần thực của z bằng 1 | b) Phần ảo của z bằng 42
5. c) Phần thực của z thuộc đoạn [-1; 2], phần ảo của z thuộc đoạn [0; 1] d) z52.

0 1 2 x

Giải a) Tập hợp các điểm thuộc đường thẳng x = 1

1. b) Tập hợp các điểm của đường thẳng y = -2 1 c) Tập hợp các điểm thuộc hình chữ nhật có các cạnh nằm trên các đường thẳng x = -1, x = 2, y = 0, y = 1 (hình gạch sọc).
2. d) Tập hợp các điểm thuộc hình tròn tâm O0; 0), bán kính bằng 2. 6. Tìm các số thực x, y sao cho: a) 3x + yi = 2y + 1 + (2 – x)i .. b) 2x + p – 1 – 1 –

Giải

(3x = 2y +1 (x=1 a) Ta có: 3x + yi=2y+1+(2-x)iew”

y = 2–x oly=1

. b) Ta có: 2x +y-1=(x + 2y -50i

(2x +y -1) + Oi = 0 +(x+2y – 5)i ::. (2x+y-1=0

(x+2y-5=0

x=-1, y = 3

7. Chứng tỏ rằng với mọi số phức z, ta luôn có phần thực và phần ảo của nó không vượt quá môđun của nó.

Giải Số phức z = a + bi, m Ta có: vao + b > vao = a2a

Va’ + ? VB? = |b|2b Vậy với mọi số phức thì phần thực cũng như phần ảo của nó không filớn hơn môđun của nó. | 8. Thực hiện các phép tính sau:

1+i a) (3+2i)[(2 –i)+(3– 2i)] b) (4 – 3i)+ *?

. 3+i 4-3i c) (1+i)? -(1-i)

2+i 2-i

2+i

Giải

1. a) Ta có: z = (3 + 2i) (5 – 3i) = 15 + 6+ (10 – 9)i = 21 + i

122:. (1+i)(2-i) b) Ta có: x=4-3i+.

1=4-3i+ -+-i =2? +12

(55) 5

23

14;

–

Il + +

–

t-i

..

–

—

1. c) Ta có: (1+i) = 1 + 2i+i =1+21-1= 2i

(1 – i)? = 1° – 21 +1? = 1 –21 – 1=-2i Vậy (1+i)-(1-1) = 2i+2O = 4i a) Ta có 3+i (3+1)(2-1) 7 1

2+i = 2+1 -5 5 4-3i_(4-3i)(2+i) 11 2; 2-

1 2° +1° -55 Vậy

3+i 4-3i_(1 1 ) (11 2:4.1;

2+i 2-i (5 5) (5 5) 9. Giải các phương trình sau trên tập số phức: a) (3 + 4i)z + (1 – 3i) = 2 + 5i b) (4 + 7i)2 – (5 – 2i) = 6iz

Giải a) Ta có: (3 + 4i)3 + (1 – 3i) = 2 + 5i

(3+4i)2 = (2+5i)-(1-3i)=1+8i

1+8i_ (1+8i)(3-4i) 7.4. FR3+41 32 +42 595 b) Ta có: (4+7i)z -(5- 2i)=6iz

(4+7i)2 – 6iz = 5-2i – (4+i)z = 5-2i > 2-5-21 _ (5–2i)(4-i) 18 13.

4* 4+1 42 +12 17 17 10. Giải các phương trình sau trên tập số phức: a) 3z2 + 7% + 8 = 0

1. b) z* – 8= 0 c) z4 – 1 = 0

Giải a) Ta có: A = 7 – 96 = -47

3z +72+8=1 02–7-i747, -7+i147 b) Đặt t =z, -8 = 0 or – 8 = 0 = = + 48 – Khi đó: 2 y = + 8 = + 48, 4, ti/8 c) 2,2 = £1, 234 = ti

–

-+-i

2

6

,22 =

N

+

11. Tìm hai số phức, biết tổng của chúng bằng 3 và tích của chúng bằng 4.

Giải Giả sử hai số phức cần tìm là Z1, Z2. Theo giả thiết ta có: sz, + Z2 =3 Sz2 =3–2, [22 = 3–2 (1) 12, 22 = 4 12 (3–2,)=4 121 – 37, + 4 =0 (2) Giải (2) ta được 2 =3tiv7 Từ (1) ta suy ra: . . .3+i77 : 3-117

2, = 172

-,

2,=

2

3+i

hoặc 2, x3-iV7,

1 2 2 12. Cho hai số phức Z1, Z2, biết rằng z1 + Z2 và Z1Z2 là hai số thực. Chứng tỏ rằng Z1, Z2 là hai nghiệm của một phương trình bậc hai với hệ số thực.

Giải Cho các số phức Z1, Z2 khi đó Z1, Z2 là các nghiệm của phương trình:

(x – 21)(x – 22) = 0 1. x, +(2, +22)x+2,22 = 0) (*)

Theo giả thiết z + Z2 và Z1Z2 là các số thực nên phương trình (*) là phương trình bậc hai với hệ số thực.