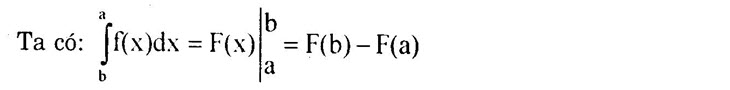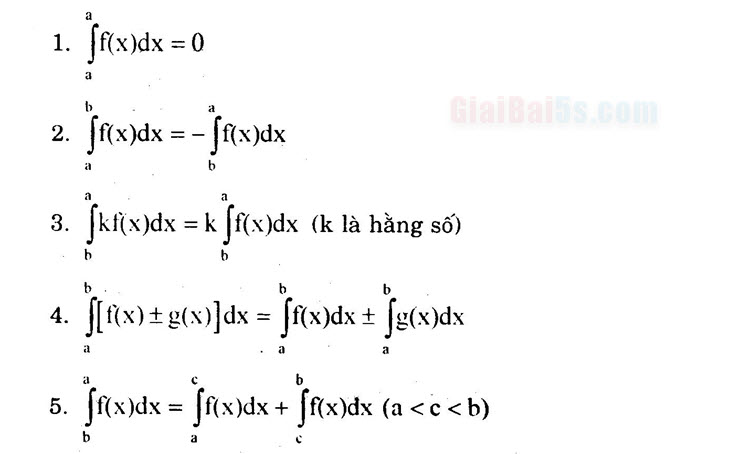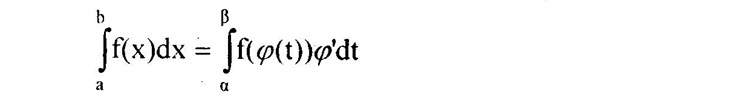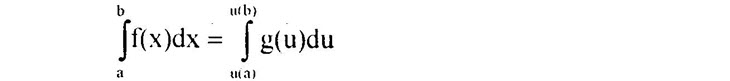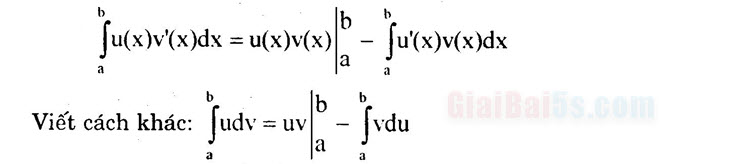| A. KIẾN THỨC CẦN NẮM VỮNG
1. Tích phân a. Diện tích của hình thang cong Cho hàm số y = f(x) liên tục trên [a; b), F(x) là một nguyên hàm của f(x) trên [a; b). Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là
Ta gọi thức dưới dấu tích phân, f(x) là hàm số dưới dấu tích phân. 2. Các tính chất
3. Phương pháp tính tích phân a. Đổi biến số Định lí 1. Cho hàm số f(x) liên tục trên [a; b]. Giả sử hàm số x = φ(t) có đạo hàm liên tục trên đoạn [α; β] sao cho φ(α) = a; φ(β) = b và a ≤ φ(t) ≤ b với mọi t ∈ [α; β]. Khi đó:
Định lí 2. Cho hàm số f(x) liên tục trên đoạn [a; b], u(x) là hàm số có đạo hàm liên tục và u(x) ∈ [a;b] và có thể viết: f(x) = g(u(x))u'(x), x € [a; b] với g(u) liên tục trên đoạn [α; β]. Khi đó ta có:
b. Tích phân từng phần Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì:
|
là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu
B. Giải bài tập
Nguồn website giaibai5s.com
- Tính các tích phân sau:
- a) Šv(1-x)’dx
–x dx
as ļte + 1dk
dy
.
.
fainzurow sin3xcos5xdx
Giải
- a) Đặt 1 – x = u; du = – da,
- b) Đặt u(x)=x, du(x) = -2x x=0=*==–
3-}ds == Janusta – con-co(-1)–(5)to bene
-x
dx = –
sin udu = cos u
=
1
X
X +
.
X-
dx = In x
– 1
ị x +1
.
:
In
–
=
– In – = In 2
X +1 i
as ļu(x+1’dx= }(x+2° + x)dt = *** |
X
16
16 – 3
+
4 +-
2
34 –
4
1- 3x
dx = |–
X+1
1
X + 1
8 In 3 + – + 3 In
ting
uln 2
—
-3-319 349 am – 4-3m 2 o įundecasuak – Bain – in2x) -Cocos x cos26
) Jacos da +_cos * * cos(-4-2) – cos(-a) – o
COS
8x + –
16
- Tính các tích phân sau:
- a) ji1xdx c) pe **+ ldx
- b) ssinRxdx d) ssin2xcos’xdx
?
Giải
[1-1 với 0 < x <1
- a) Ta có: 1 x = -1 với 1<x<2
=> ju akhir = 511 – xjóx + $(x-1)dx
=1
-+- 2 2
:
by ta ces ļain* xox = t -cos2x)dx=(1 * xin2x) *
N
1.
In
= (***-*=( 24 – 4)+(2-1) = eta
- a) Ta os. Įsim2cas sdx =2 {ainscos’adki
. –2ļeos xd (cos) –com
cos’xt
E
–
–
=0
2
0
10
- Sử dụng phương pháp đổi biến số, hãy tính:
=
X
- a) x du (đặt u = x + 1)
- (1+x)? b) |-xdx (đặt x = sint)
2dx (đặt u = 1 + xe”).
. 1 + xe
d)
, da (a>0) đặt x = asint)
va
Giải a) Đặt u = x +1=du = dx, ta có: x = 0Ởu =1;
x=3 = u = 4.
–
– J-20 +1w=ffu: +40-203)
u ?
3
3
- b) Đặt i = sint, e os dx = costat
x = 0 => t = 0;
.
:
x = 1
=
Ta cf: Mi-xidx = $w-sin” costit
– Jocosudt = } } e + cos21)dt
1.
?
- c) Đặt u =1+ xe = du xe’ (1+x)dx
x = 0 = u = 1; x= 1 Ru=1+e
X
e
ret
lite
– er
en ” – no1 * = (1+0)
1 nu
. = ln
L-dx= LG 1+ xe”
- d) Đặt x = asint = dx = a cos tdt
x= 0 => t = 0; x = * = =
Pracost
-dt=t ó acost
A dx= o va“ – X”
=
- Sử dụng phương pháp tích phân từng phần, hãy tính:
.
- b) ’Inxdx
- a) [(x+1)sin xdx c) sin(1+x)dx
P
- d) |(x2 – 2x-1)e-dx
.
Giải
.
.
.
.
- a) Đặt u(x) = x + 1, sin xdx = dv(x)
du(x)=dx, v(x)= -cosx
OS X
COS
ICO
$ex +1)sin xok ==(x +1]cps. – Serasak
– [sinx=(x+1)%e08]*2
- b) Đặt u = ln x, xdx = dv
2e +1
i
x? In xdx = -1
3
1 XP. — –dx=
3 X
li
- c) Đặt u = n(1 + x), dv =dx
= du – inv=x sin (1 + x)dx= xin (1 + x) – Banda
= n2 = (x = “n(v + x) -21021
- d) Đặt u = x? –2x+1; dv = e “dx → du = 2x – 2; v=-e*.
\\x2–2x+1)e*dx =(+*+2x+1)e*| * 236 – ude “dk
+ 28*-**2[on=vje je mar] = 2 *-1-2me “|–
- Tính các tích phân sau:
!
- a) $(1+3x) dx
- a) Đặt:
Giải u =1+3x = du = 3dx x=0= u = 1; x = 1= u = 4
== lu’du = =u?
=
☺ ☺
$(1 + 3x)}dx = 1 { u du = null – (32-1) = 3 by to osem
+x+1).
- b) Ta có:
X+1
X
-1
=
X
X
+
|
=
–
+ I In
2
1
ox-1
dx= X + 1
0
dx
—
.
V= . .
.
.
.
1+X
..
..
- c) Đặt u = \n(1 + x). dv = waktu
=> du = júnds; v=
ja s – “(19) face uyan ang Ta có: Judita dx = sifat antiox= Inv | =2in 2
…
có:
12 : : : | = 2 In 2 – In 3
— dx = In
X+1]
1 X
LX
X
+1
Thay kết quả trên vào (*) ta được: 1 = 31n
- Tính x(1-x)dx bằng hai phương pháp:
- a) Đổi biến số u = 1 − x | b) Tích phân từng phần
. . Giải a) Đổi biến số: u =1x = du =-dx; x =1-u Với x = 08 u = 1; x=1=u=0
du . .
1x(1-x) dx = – 5(-u)u’du
- b) Tính bằng phương pháp tích phân từng phần. Đặt ü= x:(1-x) dx = du = du = dx: v= (1-x)”