1. KIẾN THỨC CƠ BẢN 1. Định nghĩa | lai mặt phẳng (3), (3) được gọi là song song với nhau nếu chúng không có điểm chung.

Khi đó ta kí hiệu (a) // (3) hay (43) (a).

NCI

2. Tính chất .

– Nếu mặt phẳng (a) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (8) thì (a) song song với (B). (Đây là tính chất quan trọng để chứng minh hai mặt phẳng song song.)

fac(Q); b c(a) Ka cắt b =(a) // (8)

a // (B), b // (B) – Qua một điểm nằm ngoài mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phăng đã cho.

+ Nếu đường thẳng d song song với mặt phẳng (a) thì qua d duy nhất một mặt phẳng song song với (a).

+ Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau. . + Cho điểm A không nằm trên mặt phẳng (d). . Mọi đường thẳng đi qua A và song song với ()

đều nằm trong mặt phẳng đi qua A và song song với (a).

– Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyển song song với nhau. (Tính chất này thường xuyên được sử dụng trong các bài tập.)

– Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau.

f(a).11(B) (P) n (B) = b

(P)n(a)= a la llb 3. Định lí Ta-lét (Thales) trong không gian

| Ba mặt phẳng đổi một song song chắn trên hai cát tuyến bất kì những “đoạn thăng tương ứng tỉ lệ. • 4. Định lí Ta-lét (Thales) đảo Cho hai đường thẳng chéo nhau a và b. Trên a và b lần lượt lấy A, B, C và

• AB BC A, B, C sao cho B nằm giữa A và C, C’ nằm giữa A và B và C = 4

AB’

B’C’

an

Khi đó ba đường thẳng AA’, BB, CC lần lượt nằm trên ba mặt phẳng song song với nhau. 5. Hình lăng trụ và hình hộp

Hình lăng trụ * Hình hợp bởi các hình bình hành A,A,A,A, A,A,A,A,,…,A,A,AA và hai đa giác lồi ALA…An và AA,…A. gọi là hình lăng trụ hoặc lăng trụ, kí hiệu là AA…A..AA….A..

Nhận xét:

– Các cạnh bên của hình lăng trụ | bằng nhau và song song với nhau. a)

– Các mặt bên của hình lăng trụ là các hình bình hành. | – Hai đáy của hình lăng trụ là hai đa giác bằng nhau.

Nếu đáy của hình lăng trụ là tam giác, tứ giác, ngũ giác…thì lăng trụ tương ứng được gọi là lăng trụ tam giác, lăng trụ tứ giác, lăng trụ ngũ giác…

|

|

hình lăng trụ tam giác hình lăng trụ tứ giác hình lăng trụ lục giác Hình hộp

Hình hộp là hình lăng trụ có đáy là hình bình hành. 6. Hình chóp cụt .

| Định nghĩa – Hình chóp cụt là phần hình chóp nằm giữa đáy và thiết diện cắt bởi mặt phẳng song song với đáy hình chóp.

| Đáy của hình chóp gọi là đáy lớn của – hình chóp cụt, còn thiết diện gọi là đáy nhỏ của hình chóp cụt.

Tính chất Hình chóp cụt có:

– – Hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số

các cặp cạnh tương ứng bằng nhau. . – Các mặt bên là những hình thang. . – Các đường thẳng chứa các cạnh bên đồng quy tại một điểm. . B. HƯỚNG DẪN GIẢI BÀI TẬP (SGK) Bài 1 (Trang 71, SGK) a) Ta có: a // b và AD // BC.

mp (a, AD) // mp (b, BC). Mặt khác lại có: (A’B’C’) n (b, BC) =B’C’. Ak

B(A’B’C’) (a, AD)=0 và 1 B giao tuyến d’ qua A song song , với B’C’.

D Vì vậy qua A’ ta có thể dựng đường thẳng d’ // BC cắt d tại D sao cho A’D’ || B’C’. D’ chính là giao điểm của đường thẳng d và mp (A’B’C’). . b) Ta có: A’D || B’C’. (1) Mà (a, b) // (c, d) và AB’ = (A’B’C’D’) (a, b);

C’D’ = (A’B’C’D’) n (c,d) . Suy ra A’B’ || C’D’. (2)

Từ (1) và (2) suy ra tứ giác A’B’C’D là hình bình hành. Bài 2 (Trang 71, SGK)

1. a) Ta có: MM’ // BB’, MM’ = BB’ mà BB’ | AA’, BB’ = AA’. . . Do đó MM’ // AA’ và MM’ = AA’. Suy ra tứ giác AMM’A’ là hình bình hành. Vậy AM || A’M’. b) Gọi I là giao điểm của AM và AM’. AM’ c(ABC) và I6 AM nên I (ABC). Vậy l= A’M OKAB’C’).
2. c) Gọi O là giao điểm của AB và AB. Ta có: C và O là hai điểm chung của hai mặt phẳng (ABC) và (ABC).

| Vậy CO là giao tuyến của hai mặt phẳng (ABC) và (ABC).

ni

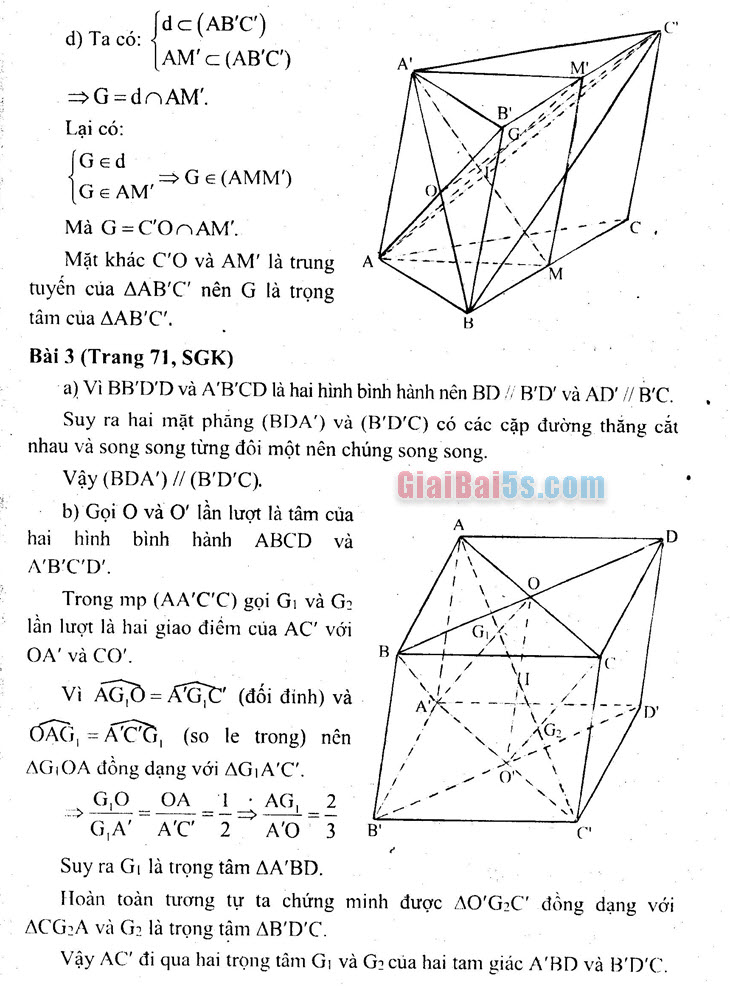
1. d) Ta có: Jdc(ABC)

‘S LAM’c(ABC) →G=dAM’. Lại có: (Ged

GEAM, →GE (AMM’)

.

|

|

Mà G=C’ON AM’.

Mặt khác CO và AM’ là trung tuyến của AAB’C’ nên G là trọng tâm của AAB’C’. Bài 3 (Trang 71, SGK)

1. a) Vì BB’DD và A’B’CD là hai hình bình hành nên BD // BD và AD // BC.

Suy ra hai mặt phẳng (BDA) và (B’DC) có các cặp đường thẳng cắt nhau và song song từng đổi một nên chúng song song.

Vậy (BDA’) // (B’D’C). . b) Gọi O và O lần lượt là tâm của hai hình bình hành ABCD và A’B’C’D’. – Trong mp (AA’C’C) gọi G và G2 lần lượt là hai giao điểm của AC với OA’ và CO. | Vì AGO = AGC (đối đỉnh) và CAC = ACG (so le trong) nên AG OA đồng dạng với AGA’C’.

GOOA 1: AG, _2 .

GA’ A’C’ 2″ A’O 3 Suy ra G là trọng tâm AA’BD. | Hoàn toàn tương tự ta chứng minh được AO’GC đồng dạng với ACG2A và G là trọng tâm AB’DC.

Vậy AC đi qua hai trọng tâm G, và G2 của hai tam giác A’BD và B’D’C.

–

BA

On

ΑΟ ΟΙ

Ca

vì AGCO đồng dạng với AG-AC) (2)

1. c) Theo trên ta có:

– (vì AGIOA đồng dạng với AG-AC’) (1)

A’C’ 2 => AG= AC Tương tự: C => CG, = AC’. Từ (1) và (2) suy ra AG = G G = GC”. d) Mp (AIO) chính là mp (AA’C’C).

= (AIO) cắt hình hộp đã cho theo thiết diện là hình bình hành AA’C’C. | Bài 4 (Trang 71, SGK) . . a) (a) // (8) // (ABCD) do đó ta có:

A,B, // A2B2 // AB; B, C; // B2C2 // BC • CDi // C2D2 // CD; A Di // A2D2 1/ AD.

A,B là đường trung bình của ASAB suy ra B là trung điểm của SB.

Chứng minh tương tự suy ra C và D lần lượt là trung điểm của SC và SD.

1. b) A2B2 là đường trung bình của hình thang ABBA nên B B2 = B2B.

B . Chứng minh tương tự suy ra CC=CC và D D = DD.

2. c) Hai hình chóp cụt có một đáy là tứ giác ABCD là A,B,C,D.ABCD và A2B2CD2.ABCD.

B,C2 // BC.

Alk17

D2.