







Nguồn website giaibai5s.com
69. Cho đường tròn (O) hai đường kính AB và CD vuông góc với nhau. Gọi M là một điểm trên cung nhỏ AC. Kẻ các dây cung MPLAB và MQ I AC.
a) Chứng minh ba điểm P, P, Q thẳng hàng ;
b) Nếu M là điểm chính giữa của cung AC thì tứ giác APQC là hình gì ? Tại sao ? Tinh các góc của tứ giác đó.
c) Chứng minh khi M chuyển động trên cung AC thì các tia phân giác trong của góc A và góc Q của tam giác MPQ luôn luôn đi qua những điểm cố định.
70. Cho đường tròn tâm O đường kính AB và điểm C là điểm chính giữa của cung AB, M là một điểm thay đổi trên cung CB. Qua C kẻ CN I AM.
a) Chứng minh tam giác MNC vuông cân ;
b) Chứng minh OCN = OAN ;
c) Điểm C ở vị trí nào trên cung BC thì tam giác OMC là tam giác đều ?
71. Cho góc nhọn xOy. Trên cạnh Ox lấy hai điểm A và B sao cho OA = 2cm, OB = 6cm, trên cạnh Oy lấy hai điểm C và D sao cho OC =1,5cm, OD = 8cm. Chứng minh :
a) AOBC AODA ;
b) Tứ giác ABDC nội tiếp được đường tròn ;
c) Góc BDC = góc OAC.
72. Cho tam giác cân ABC (AB=AC) nội tiếp đường tròn (O). Trên tia đối của các tia AB và CA lấy theo thứ tự hai điểm M và N sao cho MA = CN.
a) So sánh hai góc OAB và OCA ;
b) Chứng minh AAOM = ACON ;
c) Chứng minh tứ giác OAMN nội tiếp được đường tròn.
73. Cho tam giác ABC nội tiếp đường tròn (O). Vẽ hình bình hành ACBD. Gọi H và H lần lượt là trực tâm của tam giác ABD và ABC, còn I là trung điểm của cạnh AB. Chứng minh :
a) H thuộc đường tròn (O) và CH là đường kính của đường tròn (O).
b) Ba điểm H, I, H thẳng hàng.
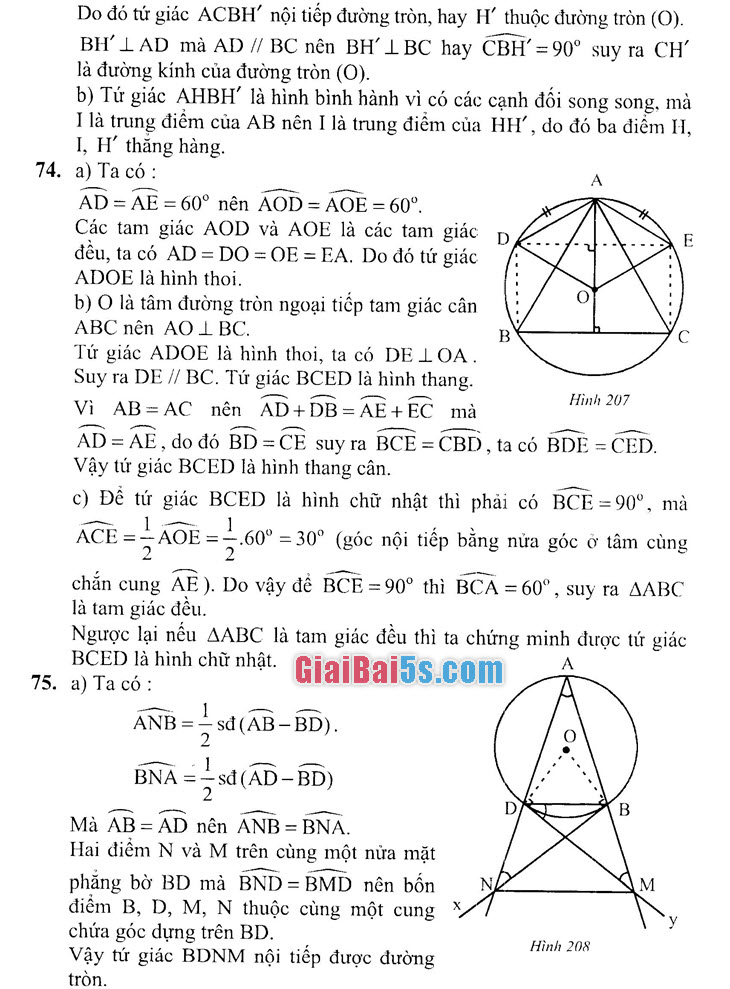
74. Cho tam giác cân ABC (AB = AC), nội tiếp đường tròn (O). Trên các cung AB và AC lấy tương ứng hai điểm D và E, biết cung AD= cung AE = 60°.
a) Tứ giác ADOE là hình gì ? Tại sao ?
b) Chứng minh tứ giác DECB là hình thang cân ;
c) Tam giác ABC cần có điều kiện gì để tứ giác DECB là hình chữ nhật ?
75. Trên đường tròn (O) lấy hai điểm B và D. Gọi A là điểm chính giữa của cung lớn BD. Các tia AD, AB cắt tiếp tuyến Bx và Dy của đường tròn lần lượt ở N và M. Chứng minh :
a) Tứ giác BDNM nội tiếp được đường tròn ;
b) MN song song với BD ;
c) MA.MB = MD2.
76. Đường kính bánh xe của một xe đạp là 65cm.
a) Bánh xe đó quay được bao nhiêu vòng khi xe đi được một đoạn đường 5km ?
b) Xe đi được bao nhiêu km khi bánh xe quay được 1500 vòng ?
77. Cho đường tròn (O), cung nhỏ AB của đường tròn có số đo 120°. Các tiếp tuyến tại A và B của đường tròn cắt nhau ở D. Vẽ đường tròn tâm P tiếp xúc với AD, BD và cung AB. Tính chu vi đường tròn (P) theo bán kính R của đường tròn (O), biết R = 12cm.
78. Cho đường tròn đường kính AD. Trên đường kính AD lấy hai điểm B và C sao cho AB = BC = CD. Vẽ các nửa đường tròn đường kính AB, AC, BD, CD như trên hình 201. Cho biết đường kính AD=12cm. Tính diện tích phần không tô màu trên hình 201.
79. Cho đường tròn (O; 5cm) và điểm M nằm bên ngoài đường tròn, biết OM = 10cm. Qua M vẽ hai tiếp tuyến MA và MB (A, B là tiếp điểm).
a) Tam giác MAB là tam giác gì ? Vì sao ?
b) Tính độ dài các cung AB của đường tròn (O);
c) Tính diện tích phần tứ giác AMB) nằm ngoài đường tròn (O).
80. Cho tam giác nhọn ABC, đường cao AH. Gọi K là điểm đối xứng với H qua AB, I là điểm đối xứng với H qua AC, E là giao điểm của KI và AB. Chứng minh rằng :
a) AICH là tứ giác nội tiếp ;
b) AI = AK;
c) Năm điểm A, E, H, C, I cùng thuộc một đường tròn ;
d) CE I AB.
HƯỚNG DẪN GIẢI – ĐÁP SỐ
69. a) Tứ giác MIOK là hình chữ nhật vì có
ô ==K = 90°, suy ra M = 90°
Do M = sdPQ nên Sa PQ = 2M =180°.
Vậy PQ là đường kính của đường tròn (O), do đó ba điểm P, 0, Q thẳng hàng.
b) AB là đường trung trực của MP nên AP = AM , suy ra AP = AM.
Tương tự MC =CQ.
Mà MA = MC, do đó AP = AM = MC=CO. CAQ= AQP (hai góc nội tiếp chắn hai cung bằng nhau CQ= AP ),
suy ra AC || PQ.
Tứ giác APQC là hình thang. Lại có APQ=CQP (hai góc nội tiếp chắn hai cung bằng nhau ACQ=PAC) nên APQC là hình thang cân.
APQ==sd (ĀC+CQ) = 4(90° + 45°) = 67°30′.
Suy ra CQP = 67°30 và PAC = ACQ=180° – 67°30′ =112°30. c
) Khi M là điểm chính giữa của cung AM thì PA + AM = MC+CO nên MP = MQ.
Tam giác MPQ là tam giác vuông cân. Khi đó phân giác của góc P đi qua điểm C cố định, còn phân giác của góc 2 đi qua điểm A cố định.
70. a) Ta có :
CMA = COA = 90° = 45° (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung ÁC ).
CNI AM nên CNM = 90°. Vậy tam giác CMN vuông cân ở N.
b) AMNC vuông cân ở N (câu a).
Ta có : NM = NC, OM = OC và cạnh ON chung. Do đó AONM = AONC (c.c.c), suy ra OMN = OCN nhưng OMN = OAN (vì AOAM là tam giác cân).
Từ đó ta có OCN = OAN. Có thể chứng minh như sau: AOC = ANC = 90° nên 0 và N thuộc đường tròn đường kính AC, do đó OCN = AN (hai góc nội tiếp cùng chắn cung ON ).
c) Tam giác OMC cân ở 0 vì có OM =OC. Tam giác OMC là tam giác đều khi CM = OM, tức là điểm M thuộc cung CB và CM = R.
7. a) Ta có :
OA_ 2 4 OD OC 1,5 3′ OB
–
=
–
—
=
8 6
—
–
4 3
Suy ra OA OD
OC OB
–
–
–
Do đó AOBC AODA (cgc)
b) Theo câu a), ta có ABC = ADC.
Hơn nữa B và D trên cùng một nửa mặt phẳng bờ AC nên bốn điểm A, C, B, D cùng thuộc một cung chứa góc dựng trên AC,
do đó tứ giác ABDC nội tiếp được đường tròn. c) Tứ giác ABDC nội tiếp đường tròn (theo câu b) nên | BDC+ BAC = 180° (hai góc đối diện của tứ giác nội tiếp), mà
BAC+CAO=180° (hai góc kề bù). Suy ra BDC=OẠC. 72. a) AO là tia phân giác của góc BAC nên
OAB=OAC. Tam giác AOC cân ở 0 nên OAC = OCA . Suy ra OAB = OCA. b) OAM+OAB = 180° OCN+OCA = 180° Mà OAB = OCA nên OAM =OCN Do đó AOAM = AOCN (c.g.c), suy ra OMA = ONC.
Hình 205
c) Hai điểm M và N trên cùng một nửa mặt phẳng bờ OA mà OMA =ONA nên bốn điểm A, 0, M, N thuộc cùng một cung chứa
góc dựng trên OA, hay tứ giác AMNO nội tiếp được đường tròn. 73. a) Ta có : ADB = A’H’B’ = 180°,
mà AHB = AHB (hai góc đối C2 đỉnh) nên
ADB + AH’B = 180o (1) Mặt khác ACB= ADB (hai góc đối diện của hình bình hành ACBD)
(2) Từ (1) và (2) suy ra ACB+AH B = 180°.
Do đó tứ giác ACBH nội tiếp đường tròn, hay Ho thuộc đường tròn (O). BHL AD mà AD // BC nên BH IBC hay CBH = 90° suy ra CH là đường kính của đường tròn (O).
b) Tứ giác AHBH là hình bình hành vì có các cạnh đối song song, mà I là trung điểm của AB nên I là trung điểm của HH, do đó ba điểm H, I, H thẳng hàng.
74. a) Ta có : AD = AE = 60° nên AOD = AOE = 60°. Các tam giác AOD và AOE là các tam giác D 2 đều, ta có AD=DO = OE = EA. Do đó tứ giác ADOE là hình thoi.
b) 0 là tâm đường tròn ngoại tiếp tam giác cân ABC nên AOI BC. Tứ giác ADOE là hình thoi, ta có DE LOA . Suy ra DE // BC. Tứ giác BCED là hình thang.
Vì AB = AC nên AD+DB = AE + EC mà AD= AE, do đó BD=CE suy ra BCE =CBD, ta có BDE = CED.
Vậy tứ giác BCED là hình thang cân.
c) Đệ tứ giác BCED là hình chữ nhật thì phải có BCE =90°, mà ACE = AOE = .60° = 30° (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung AE ).
Do vậy để BCE = 90° thì BCA = 60°, suy ra AABC là tam giác đều.
Ngược lại nếu AABC là tam giác đều thì ta chứng minh được tứ giác
BCED là hình chữ nhật. 75. a) Ta có :
ANB = – sd (AB-BD).
2
2
BNA = -så (AD-)
IN
Mà AB= AD nên ANB = BNA.
Hai điểm N và M trên cùng một nửa mặt phẳng bờ BD mà BND = BMD nên bốn điểm B, D, M, N thuộc cùng một cung chứa góc dựng trên BD.
Vậy tứ giác BDNM nội tiếp được đường tròn.
b) Tứ giác BDNM nội tiếp đường tròn, ta có BMN + BDN = 180° (hai góc đối diện của tứ giác nội tiếp)
mà BDN+ BDA = 180° (hai góc kề bù) suy ra BMN = BDA ,
nhưng BDA = DBA nên BMN = DBA.
Vậy DB // MN.
c) AMAD • AMDB (g-g) vì có góc M chung và MAD=MDB.
MA MD
“hay MA.MB = MD.
MD MB
76. Chu vi bánh xe là : C = 2TR = 3, 14.65 = 204,1 (cm)
a) Khi xe đi được 5km tức 500 000 cm, bánh xe quay được số vòng là :
500000: 204,1 = 2450 (vòng) .
b) Nếu bánh xe quay được 1500 vòng thì quãng đường xe đi được là :
204,1.1500 = 306150 (cm) ~ 3,1 km.
77. Ba điểm 0, P, D thẳng hàng.
AB=120°, do đó AOB =120°, suy ra ADB = 60°.
DO là tia phân giác của góc ADB nên ODA =JADB= 30°.
Tam giác AOD vuông ở Ả có :
ODA = 30° nên OD= 20A = 2R , suy ra
ID= R (R là bán kính đường tròn (O)).
Qua I kẻ tiếp tuyến chung với hai đường tròn cắt AD ở E, cắt BD ở F thì EF // AB (vì cùng vuông góc với OD) nên DEF = DAB = 60° và DFE = ABD= 60°.
Tam giác DEF là tam giác đều, vì thế IPO-IDER.
Vậy chu vi đường tròn (P) là : C= 2TIP = 2. 78. A = 12cm, nên AB = BC = CD = 4cm.
Gọi diện tích phần tô màu trên hình 210 là S thì S=S, TS,
Ta có S = diện tích hình tròn đường kính BD – diện tích hình tròn đường kính CD.
= 811 – 21 = 611 (cm)
Tương tự S = 6 (cm). Vậy S=S, +S, =12c (cm?)
Diện tích hình tròn đường kính AD bằng:
+ 1 = 1.62 = 361 (cm)
Diện tích phần không tô màu bằng:
361-121 = 241 = 24.3,14 = 75,36 (cm2).
79. a) Tam giác AMB cân ở M vì có MA = MB.
Tam giác AMC vuông ở A có :
OA = OM nên OMA = 30°.
Suy ra AMB = 60° Vậy tam giác AMB là tam giác đều.
b) Ta có :
AOB = 180o – AMB
= 180° – 60° = 120°
Độ dài cung nhỏ AB là :
Tt.5.120 _101 – 10,47 (cm)
“1803
Độ dài cung lớn AB là :
7.5.240 _ 2011 – 21 (cm)
180 3
c) Gọi diện tích phần phải tính là S, thì
S=SOAMB -Squạt tròn AOB SoAMB = 2S0AM = 2. -OA.AM =0A.AM
OAMB
OAM
Tam giác OAM vuông ở A :
2571
AM = OM –OA^ = 10 -5° =75, suy ra AM =53 (cm)
SOAMB = 5.5/3 = 2513
_ T.OA2.120 _ 752.120 _ 251 cm quạt tròn AOB =
360 3603 ” Vậy S= 25/3 – 7 = 43, 25-26,17 = 17,10 (cm)
80. a) AAIC = AAC (c.cc), suy ra AIC = AHC = 90°,
do đó AIC + AHC = 180°
Vậy tứ giác AICH nội tiếp được đường tròn.
b) K đối xứng với H qua AB nên AK = AH.
I đối xứng với H qua AC nên AI = AH. Suy ra AK = AI.
c) Tam giác AKI cân ở A, ta có K1 = 1 AAEH = AAEK (c.c.c) nên K = H.
Suy ra A = , do đó tứ giác AEHI nội tiếp được đường tròn.
Hai đường tròn ngoại tiếp tứ giác AHCI và AIHE cùng đi qua ba điểm A, H, I nên chúng trùng nhau.
Suy ra năm điểm A, E, H, , I cùng thuộc một đường tròn.
d) Từ câu c) suy ra AEC = AHC (hai góc nội tiếp cùng chắn cung AC), mà AHC = 90° nên AEC = 90°, do đó CEI AB.
a) Chứng minh ba điểm P, P, Q thẳng hàng ;
b) Nếu M là điểm chính giữa của cung AC thì tứ giác APQC là hình gì ? Tại sao ? Tinh các góc của tứ giác đó.
c) Chứng minh khi M chuyển động trên cung AC thì các tia phân giác trong của góc A và góc Q của tam giác MPQ luôn luôn đi qua những điểm cố định.
70. Cho đường tròn tâm O đường kính AB và điểm C là điểm chính giữa của cung AB, M là một điểm thay đổi trên cung CB. Qua C kẻ CN I AM.
a) Chứng minh tam giác MNC vuông cân ;
b) Chứng minh OCN = OAN ;
c) Điểm C ở vị trí nào trên cung BC thì tam giác OMC là tam giác đều ?
71. Cho góc nhọn xOy. Trên cạnh Ox lấy hai điểm A và B sao cho OA = 2cm, OB = 6cm, trên cạnh Oy lấy hai điểm C và D sao cho OC =1,5cm, OD = 8cm. Chứng minh :
a) AOBC AODA ;
b) Tứ giác ABDC nội tiếp được đường tròn ;
c) Góc BDC = góc OAC.
72. Cho tam giác cân ABC (AB=AC) nội tiếp đường tròn (O). Trên tia đối của các tia AB và CA lấy theo thứ tự hai điểm M và N sao cho MA = CN.
a) So sánh hai góc OAB và OCA ;
b) Chứng minh AAOM = ACON ;
c) Chứng minh tứ giác OAMN nội tiếp được đường tròn.
73. Cho tam giác ABC nội tiếp đường tròn (O). Vẽ hình bình hành ACBD. Gọi H và H lần lượt là trực tâm của tam giác ABD và ABC, còn I là trung điểm của cạnh AB. Chứng minh :
a) H thuộc đường tròn (O) và CH là đường kính của đường tròn (O).
b) Ba điểm H, I, H thẳng hàng.
74. Cho tam giác cân ABC (AB = AC), nội tiếp đường tròn (O). Trên các cung AB và AC lấy tương ứng hai điểm D và E, biết cung AD= cung AE = 60°.
a) Tứ giác ADOE là hình gì ? Tại sao ?
b) Chứng minh tứ giác DECB là hình thang cân ;
c) Tam giác ABC cần có điều kiện gì để tứ giác DECB là hình chữ nhật ?
75. Trên đường tròn (O) lấy hai điểm B và D. Gọi A là điểm chính giữa của cung lớn BD. Các tia AD, AB cắt tiếp tuyến Bx và Dy của đường tròn lần lượt ở N và M. Chứng minh :
a) Tứ giác BDNM nội tiếp được đường tròn ;
b) MN song song với BD ;
c) MA.MB = MD2.
76. Đường kính bánh xe của một xe đạp là 65cm.
a) Bánh xe đó quay được bao nhiêu vòng khi xe đi được một đoạn đường 5km ?
b) Xe đi được bao nhiêu km khi bánh xe quay được 1500 vòng ?
77. Cho đường tròn (O), cung nhỏ AB của đường tròn có số đo 120°. Các tiếp tuyến tại A và B của đường tròn cắt nhau ở D. Vẽ đường tròn tâm P tiếp xúc với AD, BD và cung AB. Tính chu vi đường tròn (P) theo bán kính R của đường tròn (O), biết R = 12cm.
78. Cho đường tròn đường kính AD. Trên đường kính AD lấy hai điểm B và C sao cho AB = BC = CD. Vẽ các nửa đường tròn đường kính AB, AC, BD, CD như trên hình 201. Cho biết đường kính AD=12cm. Tính diện tích phần không tô màu trên hình 201.
79. Cho đường tròn (O; 5cm) và điểm M nằm bên ngoài đường tròn, biết OM = 10cm. Qua M vẽ hai tiếp tuyến MA và MB (A, B là tiếp điểm).
a) Tam giác MAB là tam giác gì ? Vì sao ?
b) Tính độ dài các cung AB của đường tròn (O);
c) Tính diện tích phần tứ giác AMB) nằm ngoài đường tròn (O).
80. Cho tam giác nhọn ABC, đường cao AH. Gọi K là điểm đối xứng với H qua AB, I là điểm đối xứng với H qua AC, E là giao điểm của KI và AB. Chứng minh rằng :
a) AICH là tứ giác nội tiếp ;
b) AI = AK;
c) Năm điểm A, E, H, C, I cùng thuộc một đường tròn ;
d) CE I AB.
HƯỚNG DẪN GIẢI – ĐÁP SỐ
69. a) Tứ giác MIOK là hình chữ nhật vì có
ô ==K = 90°, suy ra M = 90°
Do M = sdPQ nên Sa PQ = 2M =180°.
Vậy PQ là đường kính của đường tròn (O), do đó ba điểm P, 0, Q thẳng hàng.
b) AB là đường trung trực của MP nên AP = AM , suy ra AP = AM.
Tương tự MC =CQ.
Mà MA = MC, do đó AP = AM = MC=CO. CAQ= AQP (hai góc nội tiếp chắn hai cung bằng nhau CQ= AP ),
suy ra AC || PQ.
Tứ giác APQC là hình thang. Lại có APQ=CQP (hai góc nội tiếp chắn hai cung bằng nhau ACQ=PAC) nên APQC là hình thang cân.
APQ==sd (ĀC+CQ) = 4(90° + 45°) = 67°30′.
Suy ra CQP = 67°30 và PAC = ACQ=180° – 67°30′ =112°30. c
) Khi M là điểm chính giữa của cung AM thì PA + AM = MC+CO nên MP = MQ.
Tam giác MPQ là tam giác vuông cân. Khi đó phân giác của góc P đi qua điểm C cố định, còn phân giác của góc 2 đi qua điểm A cố định.
70. a) Ta có :
CMA = COA = 90° = 45° (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung ÁC ).
CNI AM nên CNM = 90°. Vậy tam giác CMN vuông cân ở N.
b) AMNC vuông cân ở N (câu a).
Ta có : NM = NC, OM = OC và cạnh ON chung. Do đó AONM = AONC (c.c.c), suy ra OMN = OCN nhưng OMN = OAN (vì AOAM là tam giác cân).
Từ đó ta có OCN = OAN. Có thể chứng minh như sau: AOC = ANC = 90° nên 0 và N thuộc đường tròn đường kính AC, do đó OCN = AN (hai góc nội tiếp cùng chắn cung ON ).
c) Tam giác OMC cân ở 0 vì có OM =OC. Tam giác OMC là tam giác đều khi CM = OM, tức là điểm M thuộc cung CB và CM = R.
7. a) Ta có :
OA_ 2 4 OD OC 1,5 3′ OB
–
=
–
—
=
8 6
—
–
4 3
Suy ra OA OD
OC OB
–
–
–
Do đó AOBC AODA (cgc)
b) Theo câu a), ta có ABC = ADC.
Hơn nữa B và D trên cùng một nửa mặt phẳng bờ AC nên bốn điểm A, C, B, D cùng thuộc một cung chứa góc dựng trên AC,
do đó tứ giác ABDC nội tiếp được đường tròn. c) Tứ giác ABDC nội tiếp đường tròn (theo câu b) nên | BDC+ BAC = 180° (hai góc đối diện của tứ giác nội tiếp), mà
BAC+CAO=180° (hai góc kề bù). Suy ra BDC=OẠC. 72. a) AO là tia phân giác của góc BAC nên
OAB=OAC. Tam giác AOC cân ở 0 nên OAC = OCA . Suy ra OAB = OCA. b) OAM+OAB = 180° OCN+OCA = 180° Mà OAB = OCA nên OAM =OCN Do đó AOAM = AOCN (c.g.c), suy ra OMA = ONC.
Hình 205
c) Hai điểm M và N trên cùng một nửa mặt phẳng bờ OA mà OMA =ONA nên bốn điểm A, 0, M, N thuộc cùng một cung chứa
góc dựng trên OA, hay tứ giác AMNO nội tiếp được đường tròn. 73. a) Ta có : ADB = A’H’B’ = 180°,
mà AHB = AHB (hai góc đối C2 đỉnh) nên
ADB + AH’B = 180o (1) Mặt khác ACB= ADB (hai góc đối diện của hình bình hành ACBD)
(2) Từ (1) và (2) suy ra ACB+AH B = 180°.
Do đó tứ giác ACBH nội tiếp đường tròn, hay Ho thuộc đường tròn (O). BHL AD mà AD // BC nên BH IBC hay CBH = 90° suy ra CH là đường kính của đường tròn (O).
b) Tứ giác AHBH là hình bình hành vì có các cạnh đối song song, mà I là trung điểm của AB nên I là trung điểm của HH, do đó ba điểm H, I, H thẳng hàng.
74. a) Ta có : AD = AE = 60° nên AOD = AOE = 60°. Các tam giác AOD và AOE là các tam giác D 2 đều, ta có AD=DO = OE = EA. Do đó tứ giác ADOE là hình thoi.
b) 0 là tâm đường tròn ngoại tiếp tam giác cân ABC nên AOI BC. Tứ giác ADOE là hình thoi, ta có DE LOA . Suy ra DE // BC. Tứ giác BCED là hình thang.
Vì AB = AC nên AD+DB = AE + EC mà AD= AE, do đó BD=CE suy ra BCE =CBD, ta có BDE = CED.
Vậy tứ giác BCED là hình thang cân.
c) Đệ tứ giác BCED là hình chữ nhật thì phải có BCE =90°, mà ACE = AOE = .60° = 30° (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung AE ).
Do vậy để BCE = 90° thì BCA = 60°, suy ra AABC là tam giác đều.
Ngược lại nếu AABC là tam giác đều thì ta chứng minh được tứ giác
BCED là hình chữ nhật. 75. a) Ta có :
ANB = – sd (AB-BD).
2
2
BNA = -så (AD-)
IN
Mà AB= AD nên ANB = BNA.
Hai điểm N và M trên cùng một nửa mặt phẳng bờ BD mà BND = BMD nên bốn điểm B, D, M, N thuộc cùng một cung chứa góc dựng trên BD.
Vậy tứ giác BDNM nội tiếp được đường tròn.
b) Tứ giác BDNM nội tiếp đường tròn, ta có BMN + BDN = 180° (hai góc đối diện của tứ giác nội tiếp)
mà BDN+ BDA = 180° (hai góc kề bù) suy ra BMN = BDA ,
nhưng BDA = DBA nên BMN = DBA.
Vậy DB // MN.
c) AMAD • AMDB (g-g) vì có góc M chung và MAD=MDB.
MA MD
“hay MA.MB = MD.
MD MB
76. Chu vi bánh xe là : C = 2TR = 3, 14.65 = 204,1 (cm)
a) Khi xe đi được 5km tức 500 000 cm, bánh xe quay được số vòng là :
500000: 204,1 = 2450 (vòng) .
b) Nếu bánh xe quay được 1500 vòng thì quãng đường xe đi được là :
204,1.1500 = 306150 (cm) ~ 3,1 km.
77. Ba điểm 0, P, D thẳng hàng.
AB=120°, do đó AOB =120°, suy ra ADB = 60°.
DO là tia phân giác của góc ADB nên ODA =JADB= 30°.
Tam giác AOD vuông ở Ả có :
ODA = 30° nên OD= 20A = 2R , suy ra
ID= R (R là bán kính đường tròn (O)).
Qua I kẻ tiếp tuyến chung với hai đường tròn cắt AD ở E, cắt BD ở F thì EF // AB (vì cùng vuông góc với OD) nên DEF = DAB = 60° và DFE = ABD= 60°.
Tam giác DEF là tam giác đều, vì thế IPO-IDER.
Vậy chu vi đường tròn (P) là : C= 2TIP = 2. 78. A = 12cm, nên AB = BC = CD = 4cm.
Gọi diện tích phần tô màu trên hình 210 là S thì S=S, TS,
Ta có S = diện tích hình tròn đường kính BD – diện tích hình tròn đường kính CD.
= 811 – 21 = 611 (cm)
Tương tự S = 6 (cm). Vậy S=S, +S, =12c (cm?)
Diện tích hình tròn đường kính AD bằng:
+ 1 = 1.62 = 361 (cm)
Diện tích phần không tô màu bằng:
361-121 = 241 = 24.3,14 = 75,36 (cm2).
79. a) Tam giác AMB cân ở M vì có MA = MB.
Tam giác AMC vuông ở A có :
OA = OM nên OMA = 30°.
Suy ra AMB = 60° Vậy tam giác AMB là tam giác đều.
b) Ta có :
AOB = 180o – AMB
= 180° – 60° = 120°
Độ dài cung nhỏ AB là :
Tt.5.120 _101 – 10,47 (cm)
“1803
Độ dài cung lớn AB là :
7.5.240 _ 2011 – 21 (cm)
180 3
c) Gọi diện tích phần phải tính là S, thì
S=SOAMB -Squạt tròn AOB SoAMB = 2S0AM = 2. -OA.AM =0A.AM
OAMB
OAM
Tam giác OAM vuông ở A :
2571
AM = OM –OA^ = 10 -5° =75, suy ra AM =53 (cm)
SOAMB = 5.5/3 = 2513
_ T.OA2.120 _ 752.120 _ 251 cm quạt tròn AOB =
360 3603 ” Vậy S= 25/3 – 7 = 43, 25-26,17 = 17,10 (cm)
80. a) AAIC = AAC (c.cc), suy ra AIC = AHC = 90°,
do đó AIC + AHC = 180°
Vậy tứ giác AICH nội tiếp được đường tròn.
b) K đối xứng với H qua AB nên AK = AH.
I đối xứng với H qua AC nên AI = AH. Suy ra AK = AI.
c) Tam giác AKI cân ở A, ta có K1 = 1 AAEH = AAEK (c.c.c) nên K = H.
Suy ra A = , do đó tứ giác AEHI nội tiếp được đường tròn.
Hai đường tròn ngoại tiếp tứ giác AHCI và AIHE cùng đi qua ba điểm A, H, I nên chúng trùng nhau.
Suy ra năm điểm A, E, H, , I cùng thuộc một đường tròn.
d) Từ câu c) suy ra AEC = AHC (hai góc nội tiếp cùng chắn cung AC), mà AHC = 90° nên AEC = 90°, do đó CEI AB.
