






Nguồn website giaibai5s.com
BÀI TẬP NÂNG CAO CHƯƠNG III
81. Cho đường tròn (O), dây cung AB cố định. M là một điểm chuyển động trên cung AB. Qua trung điểm K của đoạn MB kẻ KPI AM.
Chứng minh khi M chuyển động trên cung AB thì đường thẳng KP luôn luôn đi qua một điểm cố định.
82. Cho tam giác nhọn ABC nội tiếp đường tròn (O), có BC = a, AB = b, AC = c. Gọi a, b, c là khoảng cách từ các đỉnh A, B, C đến trực tâm H của tam giác.
Chứng minh rằng các tổng ao+a; b + b và c+c” không đổi khi ba đỉnh A, B, C thay đổi trên đường tròn (O).
83. Cho hai đường tròn (O) và (0,) tiếp xúc ngoài ở K. Vẽ tiếp tuyến chung ngoài AD (A (0), De (0) )) rồi vẽ đường kính AB của đường tròn (O). Qua B vẽ tiếp tuyến BM với đường tròn (O). Chứng minh:
a) AB? = BR.BD ;
b) AB = BM.
84. Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác của các góc A, B, C cắt đường tròn (O) lần lượt ở A, B, C. Chứng minh rằng :
AA, +BB, +CC> AB+ AC+BC.
85. Cho đường tròn (O) đường kính AB và một điểm P chuyển động trên
đường tròn. Trên tia PB lấy điểm Q sao cho PQ = PA. Vẽ hình vuông APQR. Tia PR cắt đường tròn (O) ở C. “
a) Chứng minh C là tâm đường tròn ngoại tiếp AAQB ;
b) Gọi I là tâm đường tròn nội tiếp AAPB. Chứng minh bốn điểm I, A,
Q, B cùng thuộc một đường tròn.
86. Cho góc xay = 45° và điểm O nằm trong góc đó. Đường tròn (O; OA) cắt Ax, Ay lần lượt ở B và C, đường tròn đường kính BC cắt Ax, Ay lần lượt ở M và N. Chứng minh :
a) O là trực tâm của tam giác AMN ;
b) MN = BC = V2 ;
c) Sabc = 2S AMN
87. Cho đoạn thẳng AB và điểm M nằm giữa A và B. Vẽ tia Mx LAB, trên Mx lấy hai điểm C và D sao cho MC = MA và MD = MB. Đường tròn ngoại tiếp tam giác AMC và tam giác BMD cắt nhau ở N (khác M). Chứng minh :
a) Ba điểm A, N, D thẳng hàng và ba điểm M, N, C thẳng hàng ;
b) C là trực tâm của tam giác ABD
c) Đường thẳng MN luôn luôn đi qua một điểm cố định khi điểm M chuyển động trên đoạn AB.
88, Cho tam giác ABC nội tiếp đường tròn (O), phân giác của góc B cắt cạnh AC ở D, cắt đường tròn ngoại tiếp tam giác ở E. Chứng minh :
a) BD.BE = AD.AC ;
b) BD2 = AB.AC – AD.AC.
89. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O) đường kính AD. Ba đường cao AK, BL và CM cắt nhau tại H. Gọi N là giao điểm của ML với AD.
a) So sánh góc AML với góc ADB ;
b) Chứng minh tứ giác BDMN là tứ giác nội tiếp;
c) Chứng minh MLI AD.
90. Hai đường tròn (O; 5cm) và (O’; 3cm) tiếp xúc trong với nhau tại M. Tiếp tuyến của đường tròn (O) tại N cắt đường tròn (O) ở A và B. Tìm diện tích hình giới hạn bởi hai đường tròn (O), (0) và dây AB.
91. Cho hình thang ABC), A = B=90°. Một đường tròn (O) nội tiếp hình thang, tiếp xúc với đáy nhỏ BC ở M, tiếp xúc với đáy lớn AD ở N. Biết BC = r (r là bán kính đường tròn (O).
Tính diện tích phần hình thang ABCD nằm ngoài đường tròn (O).
HƯỚNG DẪN GIẢI – ĐÁP SỐ
81. Tia AO cắt đường tròn (O) ở A, thì A, là điểm cố định. MA, và KP song song với nhau vì cùng vuông góc với AM.
PK cắt BA, ở I thì KI là đường trung bình của tam giác MBA, nên I là trung điểm của BA , do đó điểm 1 cố định.
82. Tia BC cắt đường tròn (O) ở B, ta có BAB =90° (góc nội tiếp chắn nửa đường tròn đường kính BB), do đó ABI AB, suy ra AB // CH.
Tương tự CB’|| AH.
Tứ giác AHCB là hình bình hành, suy ra CB’ = AH.
Gọi M là trung điểm của BC thì OM là đường trung bình của tam giác BCB nên CB = 2OM , suy ra AH = 2OM , hay OM = AH I = -a’.
в м с
Tam giác OMB vuông ở M, ta có :
BM2+OM? = OB? hay ( +6)=R’, suy ra a’ +a” = 4R?
Tương tự bỏ +b^2 = 4R’ và c+c = 4R”, nghĩa là các tổng a? +a; b+b^ và c+c không đổi.
83. a) Dễ dàng chứng minh được ba
điểm B, K, D thẳng hàng. BDM = KMB (cùng có số đo bằng , cung KM).
Góc MBD chung. Do đó ABMKVABDM (g-g),
BK BM
Hình 215
SUV
suy ra BM
BD
(1)
AB BK
BD AB?
hay BM? = BK.BD b) AKB = 90° (góc nội tiếp chắn nửa đường tròn (O), DAB = 90°. ABK = KAD (cùng có số đo bằng , cung AK ). AAKB ADAB (g-g), suy ra AB=BA, hay ABP = BK.BD (2)
Từ (1) và (2) suy ra BM = AB , do đó BM = AB. 84. Gọi M là giao điểm của AA , BB và CC.
Góc AMB là góc ngoài tại đỉnh M của tam giác AMB, ta có: A, MB = ı + BI Mà A = u (vì AA, là phân giác của góc BAC), B2 = B (vì BB, là phân giác của góc BK3 – ABC), còn B = A2 (hai góc nội tiếp cùng
AL chắn một cung AC), do đó
Hình 216 AMB = B2 + B = ABM, vì thế tam giác AMB cân ở A, suy ra A,M+ A,B mà A, B = A,C (vì A,B=A,C). Ta có AB+ AC > BC, suy ra 2MA = AB+ AC > BC. Tương tự 2MB = BA+B,C > AC
2MC, = C,A+CB > AB Cộng theo từng vế các bất đẳng thức trên, ta được :
2(MA, + MB, + MC,) > AB+ AC + BC (1)
Mặt khác theo bất đẳng thức tam giác, ta có :
MA+MB > AB ; MB+MC > BC ; MC+MA > AC Suy ra 2(MA+MB+MC > AB+AC+ BC (2)
Từ (1) và (2), ta được : AA + BB +CC > AB + AC + BC. 85. a) PR là đường chéo của hình vuông APQR P
nên APC = BPC, suy ra CA =CB, do đó AC = BC. AAPC = AQPC (cgc), nên CA =CQ. Suy ra CA =CB=CQ. Vậy C là tâm đường tròn ngoại tiếp AAQB. b) Chúng ta dễ dàng chứng minh được AIB = AQB =135°. Từ đó suy ra bốn điểm
A, I, Q, B cùng thuộc một đường tròn. 86. a) BNC = 90° (góc nội tiếp chắn nửa
đường tròn, suy ra ANB = 90°, Tam giác ANB vuông cân ở N, do đó NB = NA nên N trên trung trực của AB. Lại có OB = C nên O trên trung trực của AB. Suy ra NO là đường trung trực của AB, do đó NOI AB, hay –
MTB NO I AM. Tương tự MOIAN. Vậy 0 là trực tâm của AAMN. b) Tứ giác OMBN là hình thang vì có OM // BN. BOC = 2BAC = 2.45° = 90°, Tam giác BOC vuông cân ở 0, ta có : OB^ + OC^ = BC?, suy ra 2MN = BC, do đó MN = BC:/2. c) Ta có MBC+MNC = 180° (hai góc đối diện của tứ giác nội tiếp). Lại có MNC+ MNA = 180° (hai góc kề bù), suy ra ABC = ANM. AABC – AAMN (g-g), ta có:
SABC _BC_/ BC L1 612_,
10
Hìn 218
N
SANM (MN) (BC: V2 = (v2)* = 2.
ANV
Vậy SABC = 2SAMN :
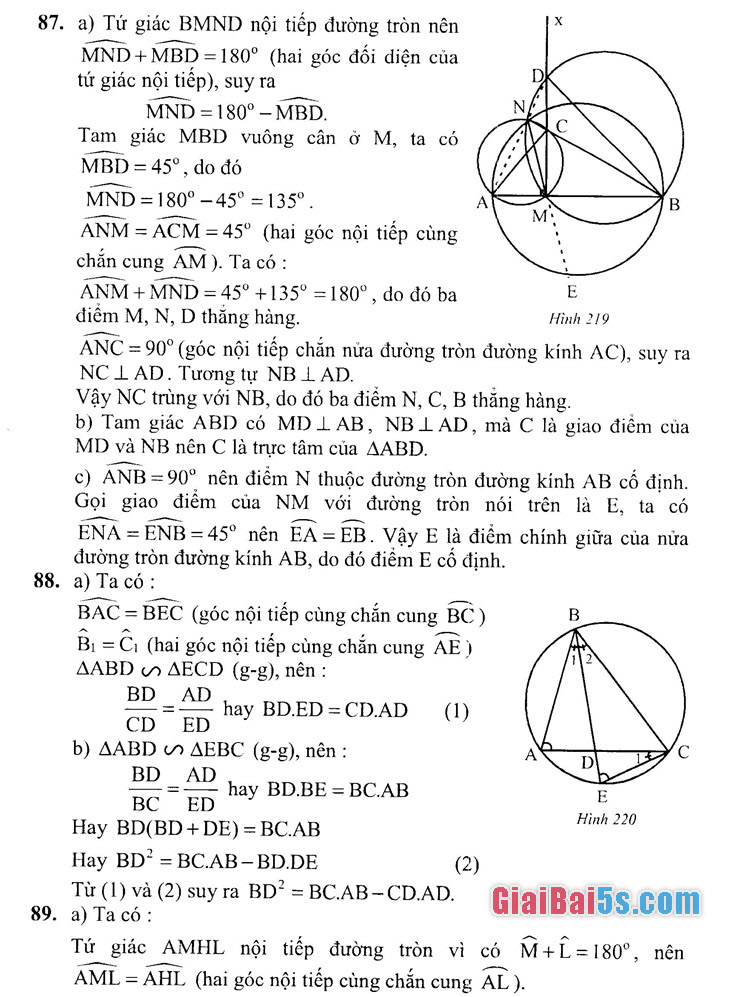
87. a) Tứ giác BMND nội tiếp đường tròn nên
MND+MBD = 180° (hai góc đối diện của tứ giác nội tiếp), suy ra
MND = 180° – MBD.
Tam giác MBD vuông cân ở M, ta có MBD= 45°, do đó MND = 180o – 45o = 1350 ANM = ACM = 45° (hai góc nội tiếp cùng chắn cung AM).
Ta có : ANM +MND = 45° +135° =180°, do đó ba điểm M, N, D thẳng hàng.
ANC = 90° (góc nội tiếp chắn nửa đường tròn đường kính AC), suy ra NCT AD. Tương tự NBI AD.
Vậy NC trùng với NB, do đó ba điểm N, C, B thẳng hàng.
b) Tam giác ABD có MDI AB, NBLAD, mà C là giao điểm của MD và NB nên C là trực tâm của AABD.
c) ANB=90o nên điểm N thuộc đường tròn đường kính AB cố định. Gọi giao điểm của NM với đường tròn nói trên là E, ta có ENA = ENB = 45° nên EA = EB.
Vậy E là điểm chính giữa của nửa đường tròn đường kính AB, do đó điểm E cố định.
88. a) Ta có :
BAC = BEC (góc nội tiếp cùng chắn cung BC) B =C (hai góc nội tiếp cùng chắn cung AE ) AABD vo AECD (g-g), nên : BD AD
AB hay BD.ED=CD.AD (1) CD ED b) AABD vo AEBC (g-g), nên :
BD AD De = n hay BD.BE = BC.AB
Hình 220 Hay BD(BD+DE) = BC.AB Hay BD- = BC.AB-BD.DE
(2) Từ (1) và (2) suy ra BD = BC.AB-CD.AD. 89. a) Ta có :
Tứ giác AMHL nội tiếp đường tròn vì có M+L = 180°, nên AML = AHL (hai góc nội tiếp cùng chắn cung AL).
DIL
AHL = ACB (vì cùng bù với góc KHL). ACB= ADB (hai góc nội tiếp cùng chắn cung AB của đường tròn (O)).
Suy ra AML = ADB.
b) BMC = BLC = 90°, do đó tứ giác BMLC nội tiếp đường tròn đường kính BC,
ta có ANG BCL+BML = 180° (hai góc đối của tứ giác nội tiếp).
Mà AML = ACB = ADB, hơn nữa AML+BML =180° (hai góc kề bù),
suy ra ADN + BMN = 180°. Tứ giác MBDN nội tiếp đường tròn.
c) Tứ giác MBDN nội tiếp đường tròn, ta có : MBD+MND=180°, mà MBD = 90°, suy ra MND = 90°, hay ML I AD
Gọi diện tích hình phải tính (phần tô màu trên hình 222) là S thì S là hiệu diện tích giữa hình tròn (O) và tổng diện tích giữa hình tròn (O) và hình viên phân AmB.
Ta có : So, = TR 2 = 16.52 = 2511 = 78,50 (cm2) Soy = nR’2 = 1.32 = 91 ~ 28, 26 (cm2)
Siến phản AnB =Squạt AOB -SAOB 00′ = 5-3 = 2 (cm); ON = 3 – 2 =1 (cm)
Tam giác DNA vuông ở N: NA” =OA? -ON = 25-1= 24, suy ra NA = V24 = 2/6 (cm), do đó AB = 2NA = 4/6 (cm). cos NOA = NO == 0, 2 suy ra NOA = 78,5°.
OA
S AOR = T.:/8,5 – 17,12 (cm2)
TIS
0
0
Hinh 222
SuᏙ Ꭲ
quat A0B
360
WAOB
SAOB = AB.ON =.476.12 4,9 (cm2)
Svjen dhan Amie ~ 17,12 – 4,9 =12, 22 (cm2) Vậy S = 78,5-(28, 26+12, 22) = 38,02 (cmỏ).
AmB
91. Tứ giác BMOE là hình vuông, ta có
B
M
C
BM = M0 =r, suy ra MC =
–
–
–
–
–
OCD+ODC = (BCD+CDA) E.
= 3.180o = 90° suy ra COD=90° ODN = MOC (vì cùng phụ với góc NC ANOD GACMO (g-g), ta có ».
– ND ON
N
Hình 223
| M0 CM, suy ra ND – MO.ON p2
CM
2r , do đó
r
AD = AN+ND=r +2r = 3r. Gọi diện tích phân phải tính là S, thì :
S = SABCD –S0; = AB.(BC+AD) – mor?
ABCD
+3r – Tr2
= 2×2 -Tr? =r?(4,5 – 1) = 1,36r?
81. Cho đường tròn (O), dây cung AB cố định. M là một điểm chuyển động trên cung AB. Qua trung điểm K của đoạn MB kẻ KPI AM.
Chứng minh khi M chuyển động trên cung AB thì đường thẳng KP luôn luôn đi qua một điểm cố định.
82. Cho tam giác nhọn ABC nội tiếp đường tròn (O), có BC = a, AB = b, AC = c. Gọi a, b, c là khoảng cách từ các đỉnh A, B, C đến trực tâm H của tam giác.
Chứng minh rằng các tổng ao+a; b + b và c+c” không đổi khi ba đỉnh A, B, C thay đổi trên đường tròn (O).
83. Cho hai đường tròn (O) và (0,) tiếp xúc ngoài ở K. Vẽ tiếp tuyến chung ngoài AD (A (0), De (0) )) rồi vẽ đường kính AB của đường tròn (O). Qua B vẽ tiếp tuyến BM với đường tròn (O). Chứng minh:
a) AB? = BR.BD ;
b) AB = BM.
84. Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác của các góc A, B, C cắt đường tròn (O) lần lượt ở A, B, C. Chứng minh rằng :
AA, +BB, +CC> AB+ AC+BC.
85. Cho đường tròn (O) đường kính AB và một điểm P chuyển động trên
đường tròn. Trên tia PB lấy điểm Q sao cho PQ = PA. Vẽ hình vuông APQR. Tia PR cắt đường tròn (O) ở C. “
a) Chứng minh C là tâm đường tròn ngoại tiếp AAQB ;
b) Gọi I là tâm đường tròn nội tiếp AAPB. Chứng minh bốn điểm I, A,
Q, B cùng thuộc một đường tròn.
86. Cho góc xay = 45° và điểm O nằm trong góc đó. Đường tròn (O; OA) cắt Ax, Ay lần lượt ở B và C, đường tròn đường kính BC cắt Ax, Ay lần lượt ở M và N. Chứng minh :
a) O là trực tâm của tam giác AMN ;
b) MN = BC = V2 ;
c) Sabc = 2S AMN
87. Cho đoạn thẳng AB và điểm M nằm giữa A và B. Vẽ tia Mx LAB, trên Mx lấy hai điểm C và D sao cho MC = MA và MD = MB. Đường tròn ngoại tiếp tam giác AMC và tam giác BMD cắt nhau ở N (khác M). Chứng minh :
a) Ba điểm A, N, D thẳng hàng và ba điểm M, N, C thẳng hàng ;
b) C là trực tâm của tam giác ABD
c) Đường thẳng MN luôn luôn đi qua một điểm cố định khi điểm M chuyển động trên đoạn AB.
88, Cho tam giác ABC nội tiếp đường tròn (O), phân giác của góc B cắt cạnh AC ở D, cắt đường tròn ngoại tiếp tam giác ở E. Chứng minh :
a) BD.BE = AD.AC ;
b) BD2 = AB.AC – AD.AC.
89. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O) đường kính AD. Ba đường cao AK, BL và CM cắt nhau tại H. Gọi N là giao điểm của ML với AD.
a) So sánh góc AML với góc ADB ;
b) Chứng minh tứ giác BDMN là tứ giác nội tiếp;
c) Chứng minh MLI AD.
90. Hai đường tròn (O; 5cm) và (O’; 3cm) tiếp xúc trong với nhau tại M. Tiếp tuyến của đường tròn (O) tại N cắt đường tròn (O) ở A và B. Tìm diện tích hình giới hạn bởi hai đường tròn (O), (0) và dây AB.
91. Cho hình thang ABC), A = B=90°. Một đường tròn (O) nội tiếp hình thang, tiếp xúc với đáy nhỏ BC ở M, tiếp xúc với đáy lớn AD ở N. Biết BC = r (r là bán kính đường tròn (O).
Tính diện tích phần hình thang ABCD nằm ngoài đường tròn (O).
HƯỚNG DẪN GIẢI – ĐÁP SỐ
81. Tia AO cắt đường tròn (O) ở A, thì A, là điểm cố định. MA, và KP song song với nhau vì cùng vuông góc với AM.
PK cắt BA, ở I thì KI là đường trung bình của tam giác MBA, nên I là trung điểm của BA , do đó điểm 1 cố định.
82. Tia BC cắt đường tròn (O) ở B, ta có BAB =90° (góc nội tiếp chắn nửa đường tròn đường kính BB), do đó ABI AB, suy ra AB // CH.
Tương tự CB’|| AH.
Tứ giác AHCB là hình bình hành, suy ra CB’ = AH.
Gọi M là trung điểm của BC thì OM là đường trung bình của tam giác BCB nên CB = 2OM , suy ra AH = 2OM , hay OM = AH I = -a’.
в м с
Tam giác OMB vuông ở M, ta có :
BM2+OM? = OB? hay ( +6)=R’, suy ra a’ +a” = 4R?
Tương tự bỏ +b^2 = 4R’ và c+c = 4R”, nghĩa là các tổng a? +a; b+b^ và c+c không đổi.
83. a) Dễ dàng chứng minh được ba
điểm B, K, D thẳng hàng. BDM = KMB (cùng có số đo bằng , cung KM).
Góc MBD chung. Do đó ABMKVABDM (g-g),
BK BM
Hình 215
SUV
suy ra BM
BD
(1)
AB BK
BD AB?
hay BM? = BK.BD b) AKB = 90° (góc nội tiếp chắn nửa đường tròn (O), DAB = 90°. ABK = KAD (cùng có số đo bằng , cung AK ). AAKB ADAB (g-g), suy ra AB=BA, hay ABP = BK.BD (2)
Từ (1) và (2) suy ra BM = AB , do đó BM = AB. 84. Gọi M là giao điểm của AA , BB và CC.
Góc AMB là góc ngoài tại đỉnh M của tam giác AMB, ta có: A, MB = ı + BI Mà A = u (vì AA, là phân giác của góc BAC), B2 = B (vì BB, là phân giác của góc BK3 – ABC), còn B = A2 (hai góc nội tiếp cùng
AL chắn một cung AC), do đó
Hình 216 AMB = B2 + B = ABM, vì thế tam giác AMB cân ở A, suy ra A,M+ A,B mà A, B = A,C (vì A,B=A,C). Ta có AB+ AC > BC, suy ra 2MA = AB+ AC > BC. Tương tự 2MB = BA+B,C > AC
2MC, = C,A+CB > AB Cộng theo từng vế các bất đẳng thức trên, ta được :
2(MA, + MB, + MC,) > AB+ AC + BC (1)
Mặt khác theo bất đẳng thức tam giác, ta có :
MA+MB > AB ; MB+MC > BC ; MC+MA > AC Suy ra 2(MA+MB+MC > AB+AC+ BC (2)
Từ (1) và (2), ta được : AA + BB +CC > AB + AC + BC. 85. a) PR là đường chéo của hình vuông APQR P
nên APC = BPC, suy ra CA =CB, do đó AC = BC. AAPC = AQPC (cgc), nên CA =CQ. Suy ra CA =CB=CQ. Vậy C là tâm đường tròn ngoại tiếp AAQB. b) Chúng ta dễ dàng chứng minh được AIB = AQB =135°. Từ đó suy ra bốn điểm
A, I, Q, B cùng thuộc một đường tròn. 86. a) BNC = 90° (góc nội tiếp chắn nửa
đường tròn, suy ra ANB = 90°, Tam giác ANB vuông cân ở N, do đó NB = NA nên N trên trung trực của AB. Lại có OB = C nên O trên trung trực của AB. Suy ra NO là đường trung trực của AB, do đó NOI AB, hay –
MTB NO I AM. Tương tự MOIAN. Vậy 0 là trực tâm của AAMN. b) Tứ giác OMBN là hình thang vì có OM // BN. BOC = 2BAC = 2.45° = 90°, Tam giác BOC vuông cân ở 0, ta có : OB^ + OC^ = BC?, suy ra 2MN = BC, do đó MN = BC:/2. c) Ta có MBC+MNC = 180° (hai góc đối diện của tứ giác nội tiếp). Lại có MNC+ MNA = 180° (hai góc kề bù), suy ra ABC = ANM. AABC – AAMN (g-g), ta có:
SABC _BC_/ BC L1 612_,
10
Hìn 218
N
SANM (MN) (BC: V2 = (v2)* = 2.
ANV
Vậy SABC = 2SAMN :
87. a) Tứ giác BMND nội tiếp đường tròn nên
MND+MBD = 180° (hai góc đối diện của tứ giác nội tiếp), suy ra
MND = 180° – MBD.
Tam giác MBD vuông cân ở M, ta có MBD= 45°, do đó MND = 180o – 45o = 1350 ANM = ACM = 45° (hai góc nội tiếp cùng chắn cung AM).
Ta có : ANM +MND = 45° +135° =180°, do đó ba điểm M, N, D thẳng hàng.
ANC = 90° (góc nội tiếp chắn nửa đường tròn đường kính AC), suy ra NCT AD. Tương tự NBI AD.
Vậy NC trùng với NB, do đó ba điểm N, C, B thẳng hàng.
b) Tam giác ABD có MDI AB, NBLAD, mà C là giao điểm của MD và NB nên C là trực tâm của AABD.
c) ANB=90o nên điểm N thuộc đường tròn đường kính AB cố định. Gọi giao điểm của NM với đường tròn nói trên là E, ta có ENA = ENB = 45° nên EA = EB.
Vậy E là điểm chính giữa của nửa đường tròn đường kính AB, do đó điểm E cố định.
88. a) Ta có :
BAC = BEC (góc nội tiếp cùng chắn cung BC) B =C (hai góc nội tiếp cùng chắn cung AE ) AABD vo AECD (g-g), nên : BD AD
AB hay BD.ED=CD.AD (1) CD ED b) AABD vo AEBC (g-g), nên :
BD AD De = n hay BD.BE = BC.AB
Hình 220 Hay BD(BD+DE) = BC.AB Hay BD- = BC.AB-BD.DE
(2) Từ (1) và (2) suy ra BD = BC.AB-CD.AD. 89. a) Ta có :
Tứ giác AMHL nội tiếp đường tròn vì có M+L = 180°, nên AML = AHL (hai góc nội tiếp cùng chắn cung AL).
DIL
AHL = ACB (vì cùng bù với góc KHL). ACB= ADB (hai góc nội tiếp cùng chắn cung AB của đường tròn (O)).
Suy ra AML = ADB.
b) BMC = BLC = 90°, do đó tứ giác BMLC nội tiếp đường tròn đường kính BC,
ta có ANG BCL+BML = 180° (hai góc đối của tứ giác nội tiếp).
Mà AML = ACB = ADB, hơn nữa AML+BML =180° (hai góc kề bù),
suy ra ADN + BMN = 180°. Tứ giác MBDN nội tiếp đường tròn.
c) Tứ giác MBDN nội tiếp đường tròn, ta có : MBD+MND=180°, mà MBD = 90°, suy ra MND = 90°, hay ML I AD
Gọi diện tích hình phải tính (phần tô màu trên hình 222) là S thì S là hiệu diện tích giữa hình tròn (O) và tổng diện tích giữa hình tròn (O) và hình viên phân AmB.
Ta có : So, = TR 2 = 16.52 = 2511 = 78,50 (cm2) Soy = nR’2 = 1.32 = 91 ~ 28, 26 (cm2)
Siến phản AnB =Squạt AOB -SAOB 00′ = 5-3 = 2 (cm); ON = 3 – 2 =1 (cm)
Tam giác DNA vuông ở N: NA” =OA? -ON = 25-1= 24, suy ra NA = V24 = 2/6 (cm), do đó AB = 2NA = 4/6 (cm). cos NOA = NO == 0, 2 suy ra NOA = 78,5°.
OA
S AOR = T.:/8,5 – 17,12 (cm2)
TIS
0
0
Hinh 222
SuᏙ Ꭲ
quat A0B
360
WAOB
SAOB = AB.ON =.476.12 4,9 (cm2)
Svjen dhan Amie ~ 17,12 – 4,9 =12, 22 (cm2) Vậy S = 78,5-(28, 26+12, 22) = 38,02 (cmỏ).
AmB
91. Tứ giác BMOE là hình vuông, ta có
B
M
C
BM = M0 =r, suy ra MC =
–
–
–
–
–
OCD+ODC = (BCD+CDA) E.
= 3.180o = 90° suy ra COD=90° ODN = MOC (vì cùng phụ với góc NC ANOD GACMO (g-g), ta có ».
– ND ON
N
Hình 223
| M0 CM, suy ra ND – MO.ON p2
CM
2r , do đó
r
AD = AN+ND=r +2r = 3r. Gọi diện tích phân phải tính là S, thì :
S = SABCD –S0; = AB.(BC+AD) – mor?
ABCD
+3r – Tr2
= 2×2 -Tr? =r?(4,5 – 1) = 1,36r?
