I. KIẾN THỨC CẦN NHỚ
| • Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn (một cung nằm giữa hai cạnh của góc và cung kia nằm giữa các tia đối của hai cạnh ấy).
• Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn giữa hai cạnh của góc đó. |





Nguồn website giaibai5s.com
Ví dụ 6: Trên đường tròn (O) lấy theo thứ tự bốn điểm A, B, C, D sao cho AB=100°, BC = 30°, CD = 60°.
a) Tính các góc của tứ giác ABCD ;
b) Gọi I và J lần lượt là giao điểm của AB và DC, của AC và BD. Tính các góc AID và AJD.
Giải:
a) Ta có : så AD = 360° – (sđ AB+så BC+så CD)
= 360° – (100° +30° +60°) = 170°
DAB = (sđ BC + SACD)
= {(30° +60°)= 45°
ADC =4(sđ AB+ sđ BC)
= (1000 +30°) = 65°
ABC = {(sd AD + sd DC)={(170° +60°) =115″
DCB=(sd AD + sd AB)=L(170° +100”)=135°
b) Góc AID là góc có đỉnh nằm bên ngoài đường tròn (O), ta có :
AID = (sd AD- sđ BC) = 170° – 30° =70°
Góc AJD là góc có đỉnh nằm bên trong đường tròn (O), ta có :
AJD = = (sd AD + sd BC) = 4(170° +30°) = 100°
II. BÀI TẬP
30. Cho tam giác ABC nội tiếp đường tròn (O), có B= 46°, C=72°.
a) Tính góc A của tam giác ABC ;
b) Tia phân giác của góc A cắt đường tròn ở M, tia phân giác của góc B cắt đường tròn ở N. Gọi I là giao điểm của AM và BN. Tính các góc BIM và MBI ;
c) Chứng minh MB = MC = MI.
31. Cho tam giác ABC cân ở A nội tiếp đường tròn (O). Tia phân giác của góc B cắt đường tròn ở D, tia phân giác của góc C cắt đường tròn ở F. Gọi E là giao điểm của BD và CF.
Tứ giác ADEF là hình gì ? Vì sao ?
32. Cho đường tròn (O), hai dây cung AB và AC.
a) Gọi I và J theo thứ tự là điểm chính giữa của cung AB và cung AC. Đường thẳng IJ cắt AB và AC lần lượt ở K và H. Chứng minh AK = AH ;
b) Trường hợp AB= AC. Gọi M là một điểm thuộc cung nhỏ AC, S là giao điểm của AM và BC. Chứng minh ASC == MCA.
33. Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn. Từ M kẻ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC tới đường tròn. Phân giác của góc BAC cắt BC ở D, cắt đường tròn ở E. Chứng minh: a) MA = MD ;
b) AD.AE = AC.AB.
34. Cho đường tròn (O) và điểm S nằm bên ngoài đường tròn. Từ S kẻ hai tiếp tuyến SA và SA (A và A là tiếp điểm) và cát tuyến SBC tới đường tròn. Phân giác của góc BAC cắt BC ở D, cắt đường tròn ở E. Gọi H là giao điểm của OS và AA”, G là giao điểm của OE và BS còn F là giao điểm của AA’ với BC. Chứng minh :
a) Tam giác SAD là tam giác cân ;
b) SF.SG = SOSH ;
c) SA? =SF.SG
35. Qua điểm A nằm bên ngoài đường tròn (O), kẻ hai cát tuyến ABC và AMN. Hai đường thăng BN và CM cắt nhau ở S. Chứng minh :
a) A+BSM = 2CBN ;
b) AM.AN = AB.AC.
III. HƯỚNG DẪN GIẢI – ĐÁP SỐ
30. a) = 180o – (+Ĉ)
= 180o – (46° + 72°) = 62°
b) Do B = 46° nên SC AC=2.46° =92° A = 62° nên sử BC = 2.62° =1249
AM là tia phân giác của góc A nên MAB = MẠC,
suy ra MB=MC = BC BN là tia phân giác của góc B nên NBA = NBC ,
suy ra NA = NC-AC
M
linh 157
yr
+
MBI = -sd (MC + NO
(124° +92°)
2
-= 540
MB = _st (MC + NT) = _w BEAC 1 024 792″) = 54″ MTB = sa (MB+ NA) = -sd BC +ĀC _ ! (124° +92°) – 540
N
2
2
c) Vì MBI = MIB(= 54°), do đó AMIB cân ở M, suy ra MB =MI.
Vì MB = MC nên MB=MC.
Suy ra MB = MC = MI. 31. BD là phân giác của góc B nên B = B2,
CF là phân giác của góc C nên C = C.
Mà B=c, do đó B = B = =Cy, suy ra AF = BF= AD =DC.
AFC = -sd(AD+DC)
DEC = -sd (BF +CD)
Suy ra AFC =DEC, do đó AF // ED (hai góc ở vị trí đồng vị bằng nhau).
Tương tự AD // EF. Tứ giác ADEF có các cạnh đối song song nên là hình bình hành.
Do AF = AD nên AF=AD vì thế ADEF là hình thoi.
32. a) AKH = G(AJ +1B),
AHK = s(TC+1) Mà theo giá thiết thì AI = IB và AJ =IC nên
[/ B
AKH = AHK. Vậy tam giác AHK cân ở A, ta có AH = AK (h. 159).
Hình 159
b) MCA = -sd AM,
ASC=s(AB-MC) Theo giả thiết AB = AC nên
AB = AC, do đó ASC = s(AC-MC)
= LsdĀM. Vậy MCA = ASC (1.160). 33. a) MAE = sd (AB + BE) ; MDA = Lsd (AB+CE)
Vì AE là tia phân giác của góc BAC nên BAE =CAE, suy ra BE =CE.
Do đó MAE = MDA, thế thì tam giác AMD cân ở M, ta có MA = MD.
b) ACD = AEB (hai góc nội tiếp cùng chắn cung AB). CAD = BAE (theo câu a).
Vay ΔΑCD ΔΑΕΒ (g-g),
CLB AC AD suy ra
AE AB hay AD.AE = AB.AC
34. a) Tương tự câu a) bài 33, tam giác SAD cân ở S.
b)OC = OB nên O nằm trên đường trung trực của BC. EB = EC nên EB = EC, E nằm trên đường trung trực của BC.
Suy ra OE là đường trung trực của BC, do đó OE I BC.
SO là tia phân giác của tam giác cân ASA nên SHI AA”.
Hình 162 AOGS (AFHS (9-9), ta có SG = hay SO.SH=SF.SG
SH SF
c) Tam giác OAS vuông ở A, có AH IOS nên SA? =SHIOS.
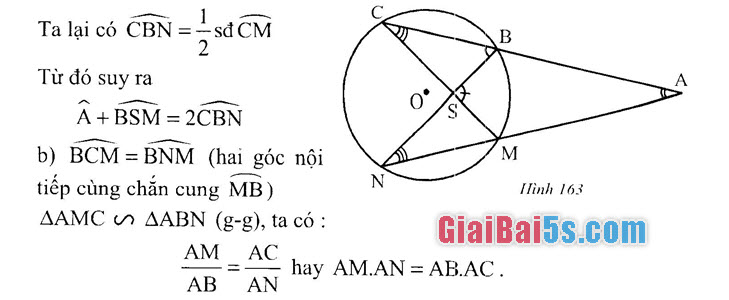
Kết hợp với câu b), ta có SA? =SFSG. 35. a) Ta có : =sa (CN – BM); BSM = sa (CN + BM)
Vậy A + BSM = sd(CN-BM + CN + BM) =sdCN
Ta lại có CBN = số CM.
Từ đó suy ra
A + BSM = 2CBN
b) BCM – BNM (hai góc nội
M
N tiếp cùng chắn cung MB) SAMC – AABN (g-g), ta có :
AM AC
= = hay AM.AN = AB.AC.
Ilinh 163
AB AN
a) Tính các góc của tứ giác ABCD ;
b) Gọi I và J lần lượt là giao điểm của AB và DC, của AC và BD. Tính các góc AID và AJD.
Giải:
a) Ta có : så AD = 360° – (sđ AB+så BC+så CD)
= 360° – (100° +30° +60°) = 170°
DAB = (sđ BC + SACD)
= {(30° +60°)= 45°
ADC =4(sđ AB+ sđ BC)
= (1000 +30°) = 65°
ABC = {(sd AD + sd DC)={(170° +60°) =115″
DCB=(sd AD + sd AB)=L(170° +100”)=135°
b) Góc AID là góc có đỉnh nằm bên ngoài đường tròn (O), ta có :
AID = (sd AD- sđ BC) = 170° – 30° =70°
Góc AJD là góc có đỉnh nằm bên trong đường tròn (O), ta có :
AJD = = (sd AD + sd BC) = 4(170° +30°) = 100°
II. BÀI TẬP
30. Cho tam giác ABC nội tiếp đường tròn (O), có B= 46°, C=72°.
a) Tính góc A của tam giác ABC ;
b) Tia phân giác của góc A cắt đường tròn ở M, tia phân giác của góc B cắt đường tròn ở N. Gọi I là giao điểm của AM và BN. Tính các góc BIM và MBI ;
c) Chứng minh MB = MC = MI.
31. Cho tam giác ABC cân ở A nội tiếp đường tròn (O). Tia phân giác của góc B cắt đường tròn ở D, tia phân giác của góc C cắt đường tròn ở F. Gọi E là giao điểm của BD và CF.
Tứ giác ADEF là hình gì ? Vì sao ?
32. Cho đường tròn (O), hai dây cung AB và AC.
a) Gọi I và J theo thứ tự là điểm chính giữa của cung AB và cung AC. Đường thẳng IJ cắt AB và AC lần lượt ở K và H. Chứng minh AK = AH ;
b) Trường hợp AB= AC. Gọi M là một điểm thuộc cung nhỏ AC, S là giao điểm của AM và BC. Chứng minh ASC == MCA.
33. Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn. Từ M kẻ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC tới đường tròn. Phân giác của góc BAC cắt BC ở D, cắt đường tròn ở E. Chứng minh: a) MA = MD ;
b) AD.AE = AC.AB.
34. Cho đường tròn (O) và điểm S nằm bên ngoài đường tròn. Từ S kẻ hai tiếp tuyến SA và SA (A và A là tiếp điểm) và cát tuyến SBC tới đường tròn. Phân giác của góc BAC cắt BC ở D, cắt đường tròn ở E. Gọi H là giao điểm của OS và AA”, G là giao điểm của OE và BS còn F là giao điểm của AA’ với BC. Chứng minh :
a) Tam giác SAD là tam giác cân ;
b) SF.SG = SOSH ;
c) SA? =SF.SG
35. Qua điểm A nằm bên ngoài đường tròn (O), kẻ hai cát tuyến ABC và AMN. Hai đường thăng BN và CM cắt nhau ở S. Chứng minh :
a) A+BSM = 2CBN ;
b) AM.AN = AB.AC.
III. HƯỚNG DẪN GIẢI – ĐÁP SỐ
30. a) = 180o – (+Ĉ)
= 180o – (46° + 72°) = 62°
b) Do B = 46° nên SC AC=2.46° =92° A = 62° nên sử BC = 2.62° =1249
AM là tia phân giác của góc A nên MAB = MẠC,
suy ra MB=MC = BC BN là tia phân giác của góc B nên NBA = NBC ,
suy ra NA = NC-AC
M
linh 157
yr
+
MBI = -sd (MC + NO
(124° +92°)
2
-= 540
MB = _st (MC + NT) = _w BEAC 1 024 792″) = 54″ MTB = sa (MB+ NA) = -sd BC +ĀC _ ! (124° +92°) – 540
N
2
2
c) Vì MBI = MIB(= 54°), do đó AMIB cân ở M, suy ra MB =MI.
Vì MB = MC nên MB=MC.
Suy ra MB = MC = MI. 31. BD là phân giác của góc B nên B = B2,
CF là phân giác của góc C nên C = C.
Mà B=c, do đó B = B = =Cy, suy ra AF = BF= AD =DC.
AFC = -sd(AD+DC)
DEC = -sd (BF +CD)
Suy ra AFC =DEC, do đó AF // ED (hai góc ở vị trí đồng vị bằng nhau).
Tương tự AD // EF. Tứ giác ADEF có các cạnh đối song song nên là hình bình hành.
Do AF = AD nên AF=AD vì thế ADEF là hình thoi.
32. a) AKH = G(AJ +1B),
AHK = s(TC+1) Mà theo giá thiết thì AI = IB và AJ =IC nên
[/ B
AKH = AHK. Vậy tam giác AHK cân ở A, ta có AH = AK (h. 159).
Hình 159
b) MCA = -sd AM,
ASC=s(AB-MC) Theo giả thiết AB = AC nên
AB = AC, do đó ASC = s(AC-MC)
= LsdĀM. Vậy MCA = ASC (1.160). 33. a) MAE = sd (AB + BE) ; MDA = Lsd (AB+CE)
Vì AE là tia phân giác của góc BAC nên BAE =CAE, suy ra BE =CE.
Do đó MAE = MDA, thế thì tam giác AMD cân ở M, ta có MA = MD.
b) ACD = AEB (hai góc nội tiếp cùng chắn cung AB). CAD = BAE (theo câu a).
Vay ΔΑCD ΔΑΕΒ (g-g),
CLB AC AD suy ra
AE AB hay AD.AE = AB.AC
34. a) Tương tự câu a) bài 33, tam giác SAD cân ở S.
b)OC = OB nên O nằm trên đường trung trực của BC. EB = EC nên EB = EC, E nằm trên đường trung trực của BC.
Suy ra OE là đường trung trực của BC, do đó OE I BC.
SO là tia phân giác của tam giác cân ASA nên SHI AA”.
Hình 162 AOGS (AFHS (9-9), ta có SG = hay SO.SH=SF.SG
SH SF
c) Tam giác OAS vuông ở A, có AH IOS nên SA? =SHIOS.
Kết hợp với câu b), ta có SA? =SFSG. 35. a) Ta có : =sa (CN – BM); BSM = sa (CN + BM)
Vậy A + BSM = sd(CN-BM + CN + BM) =sdCN
Ta lại có CBN = số CM.
Từ đó suy ra
A + BSM = 2CBN
b) BCM – BNM (hai góc nội
M
N tiếp cùng chắn cung MB) SAMC – AABN (g-g), ta có :
AM AC
= = hay AM.AN = AB.AC.
Ilinh 163
AB AN
