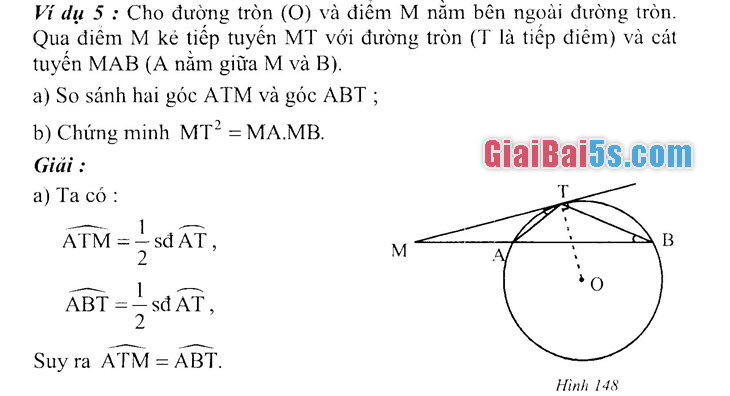
Ví dụ 5 : Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn. Qua điểm M kẻ tiếp tuyến MT với đường tròn (T là tiếp điểm) và cát tuyến MAB (A nằm giữa M và B).
a) So sánh hai góc ATM và góc ABT ;
b) Chứng minh MT? = MA.MB.
Giải: a) Ta có :
ATM=-sd AT,
ABT = = sdĀT, Suy ra ATM = ABT.
Chú ý: Qua chứng minh trên, ta có thể rút ra nhận xét sau: “Trong một đường tròn góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau”.
b) AMAT và AMTB có góc M chung, MTA = MBT (theo câu a). Do đó AMAT AMTB (g-g), ta có:
MA MT
, suy ra MT = MA.MB. MT MB’
II. BÀI TẬP
23. Cho hai đường tròn (O) và đường tròn (O) tiếp xúc ngoài tại điểm A. Qua A kẻ một cát tuyến cắt đường tròn (O) ở B, cắt đường tròn (O’) ở C. Gọi BD và CE là dây cung của đường tròn (O) và (O’). Biết BD // CE.
a) So sánh các cung nhỏ AB và AE của đường tròn (O) và (0) ;
b) Kẻ tiếp tuyến chung trong xAx của hai đường tròn tại A (tia Ax thuộc nửa mặt phẳng bờ 00 chứa điểm D). So sánh hai góc DAx và góc EAx , từ đó chứng minh ba điểm A, E, D thẳng hàng.
24. Cho hai đường tròn (O) và (O’) cắt nhau ở A và B (0 và 0 thuộc hai nửa mặt phẳng bờ AB). Qua A kẻ cát tuyến cắt đường tròn (O) ở C, cắt đường tròn (O) ở D. Các tiếp tuyến của hai đường tròn kẻ từ C và D cắt nhau ở I. Chứng minh khi cát tuyến CAD thay đổi thì:
a) Góc CBD không đổi ;
b) Góc CID không đổi.
25. Cho đường tròn (O), dây cung MN, tiếp tuyến Mx. Trên Mx lấy điểm T sao cho MT = MN . Đường thẳng TN cắt đường tròn ở S. Chứng minh :
a) SMT = † ;
b) SM = ST.
26. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài ở A. Một cát tuyến kẻ qua A cắt đường tròn (O) ở B, cắt đường tròn (O) ở C. Kẻ các đường kính BD và CE của hai đường tròn (O) và (O’).
a) Chứng minh ba điểm D, A, E thẳng hàng ;
b) Chứng minh BD || CE,
c) Nếu đường tròn (O) bằng đường tròn (O) thì tứ giác BDCE là hình gì ? Vì sao ?
27. Cho đường tròn (O) đường kính AB và một điểm C trên nửa đường | tròn. Qua C kẻ đường thẳng song song với AB cắt đường tròn ở D. Kẻ CHICD. Chứng minh :
a) AH là tiếp tuyến của đường tròn (O);
b) ACD = DAH ;
c) AH= HC.HD.
28. Cho nửa đường tròn (O) đường kính AB và một điểm C trên nửa đường tròn. Qua điểm D trên đoạn AB kẻ đường thẳng vuông góc với AB, cắt BC ở F. Tiếp tuyến của nửa đường tròn tại C cắt đường vuông góc ở D tại I. Gọi E là giao điểm của AC và DF.
a) So sánh góc IEC với góc ICE và góc ABC ;
b) Chứng minh tam giác EIC là tam giác cân ;
c) Chứng minh IE = IC = IF.
29. Cho nửa đường tròn (O) đường kính AB, tiếp tuyến Ax. Gọi C là một điểm trên nửa đường tròn. Tia phân giác của góc CAx cắt nửa đường tròn ở E, AE và BC cắt nhau ở K.
a) Tam giác ABK là tam giác gì ? Vì sao ?
b) Gọi I là giao điểm của AC và BE. Chứng minh KI || Ax ; | c) Chứng minh OE // BC.
III. HƯỚNG DẪN GIẢI – ĐÁP SỐ
23. a) Trong đường tròn (O):
Ê = -sd AD. Trong đường tròn (O’) :
2
OT
LO:
© = _ sa At.
Hình 149
Do BD // CE nên B=C (hai góc so le B trong). Suy ra sđ AD = số AE.
b) Trong đường tròn (O):
B= DAx (vì cùng bằng sử AD). Trong đường tròn (O):
C=xAE (vì cùng bằng sứ AE ). Mà B=C nên DAx = EAx. Vì xAD+DAx =180°, do đó DAx +xAE = 180°. Vậy ba điểm D, A,
E thẳng hàng. 24. a) Trong đường tròn (O) :
BCD = – sd AmB. Trong đường tròn (O) :
BDC = – sd AnB. Vì đường tròn (O) và (O’) cắt nhau , tại hai điểm A và B cho trước nên các cung AB và AnB không đổi do đó BCD và BDC không đổi, vì thế trong tam giác BCD ta có góc CBD không đổi. b) Trong đường tròn (O):
ABC = ACI (vì cùng bằng sơ AC). Trong đường tròn (O) :
ABD = ADI (vì cùng bằng sự AD ). Suy ra ICD+ IDC = CBA + ABD=CBD không đổi, từ đó suy ra góc
CID không đổi. 25. a) Ta có :
S= M (vì cùng bằng ssd MN ). Do đó SMT = M + M = S+ Mg. Góc MNT là góc ngoài ở đỉnh N của tam giác SNM, ta có MNT =$+M2.
Hình 15)
Suy ra SMT = MNT (1)
Tam giác MNT cần ở M nên MNT=MTN (2)
Từ (1) và (2) suy ra 1= SMT.
b) Tam giác SMT cân ở S vì có T=M, do đó s ST = SM.
Hình 151
26. a) BAD = 90° (góc nội tiếp chắn nửa đường tròn (O)).
CAE = 90° (góc nội tiếp chắn nửa đường tròn (O’)).
Suy ra DAB+CAE = BAE + EAC=180°, do đó ba điểm D, A, E thẳng hàng.
b) Tam giác AOD cân ở 0, ta có : OAD = ODA.
Tam giác OAE cân ở 0, ta có : O’AE = OʻEA. Mà OAD=0AE (hai góc đối đỉnh), B do đó BD // CE.
Cách khác : Qua A kẻ tiếp tuyến chung xx , ta có :
D = BAx (cùng bằng ; sđ AB). Ê=CAx (cùng bằng 1 sảAC).
x
Hình 152
Mà BAx =CAx (hai góc đối đỉnh), suy ra D= E. Do đó BD || CE.
c) Nếu đường tròn (O) bằng đường tròn (O) thì BD=CE.
Tứ giác BDCE có hai cạnh đối vừa song song vừa bằng nhau nên là hình bình hành.
Mặt khác BCIDE, do vậy tứ giác BDCE là hình thoi.
27. a) AH LCD mà CD AB nên AHI AB tại A. Do đó AH là tiếp
tuyến của đường tròn (O) tại điểm A.
b) ACD=DAH (vì cùng bằng số AD). c) AAHCADHA (g-g), ta có : AH HC
S hay AH = HC.HD.
O
HD HA
Hình 153
F
28. a) ACB=90° (góc nội tiếp chắn nửa đường tròn (O), suy ra ECF = 90° (hai góc kề bù).
DF LAB nên BDF = 90°.
Hai tam giác vuông CEF và DBF có chung góc F nên ABC = IEC.
Mặt khác ABC = ICE (cùng bằng ssd AC).
Suy ra IEC = ICE = ABC.
D O
Hình : 54
b) Tam giác IEC cân ở I vì có IEC = ICE nên IE =IC. (1)
c) Ta có : C +ICE =90° và f+IEC = 90° mà ICE = IEC, do đó C =F.
Tam giác ICF cân ở I, ta có IC = IF. (2) Từ (1) và (2) suy ra IE = IC= IF.
29. a) AEB=90° (góc nội tiếp chắn nửa đường XL
tròn (O), suy ra BE I AK. B = A (cùng bằng sự AE ).
B= u (hai góc nội tiếp cùng chắn cung
EK
:
EC).
CU
Mà A = u nên B = B. hay BE là phân
O giác của góc ABK.
Hình 155 Tam giác ABK có BE vừa là đường cao vừa là phân giác nền AABK cân ở B.
b) ACB = 90° (góc nội tiếp chắn nửa đường tròn (O)) nên ACI BK.
I là giao điểm hai đường cao trong tam giác AKB nên I là trực tâm của. tam giác đó, ta có KII AB, mà AxlAB. Suy ra KI || Ax.
c) Vì A = u nên AE = EC, suy ra EA = EC.
Vậy điểm E nằm trên đường trung trực của AC
Mặt khác OA = OC nên 2 nằm trên đường trung trực của AC.
Do đó OE là đường trung trực của AC, suy ra OEL AC, nhưng BCI AC vì thế OE // BC.