I. KIẾN THỨC CẦN NHỚ
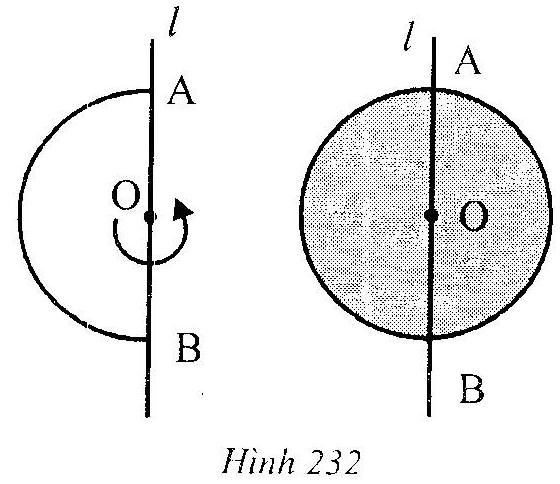
| • Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu (hình 232).
– Điểm O được gọi là tâm, độ dài R là bán kính của hình cầu. – Nửa đường tròn trong phép quay nói trên tạo nên mặt cầu. |
 |
| • Khi cắt hình cầu bán kính R bởi một mặt phẳng, ta được : – Một đường tròn bán kính R nếu mặt phẳng đi qua tấm hình cầu (gọi là đường tròn lớn). – Một đường tròn bán kính bé hơn R nếu mặt phẳng không đi qua tâm hình cầu. • Diện tích mặt cầu : S= 4πR2 hay S = πd2 R là bán kính, d là đường kính mặt cầu. • Thể tích hình cầu : V= 4/3 πR3 |
|



Nguồn website giaibai5s.com
Ví dụ 1: Một mặt cầu có diện tích 72,35 cm”. Một mặt cầu thứ hai có bán kính bằng bán kính của mặt cầu này. Hãy tính diện tích mặt cầu thứ hai (lấy = 3,14).
Giải:
Gọi R, là bán kính của mặt cầu thứ nhất, ta có : 4TR =72,35 suy ra R =72,35=72,35 – -5,76
41 4.3.14 do đó R = 2,4 (cm).
Gọi R, là bán kính của mặt cầu thứ hai thì :
R = R1 = 2,4 = 0,8 (cm)
Diện tích mặt cầu thứ hai là :
S = 47R3 = 4.17.0,8° = 2,5611~8,04 (cm2).
Ví dụ 2 :Một hình trụ có bán kính đường tròn đáy là 5cm, chiều cao 6cm. Một hình cầu có thể tích bằng – thể tích hình trụ nói trên. Hãy tính bán kính hình cầu. (Lấy T = 3,14 ).
Giải:
Thể tích hình trụ là : V = h =T.5.6=150 (cm) Vì thể tích hình cầu bằng , thể tích hình trụ nên thể tích hình cầu là :
3
15017.2 = 1001 (cm)
Gọi R là bán kính hình cầu, ta có : 4 =100,
suy ra 4TR = 300
hay R3 = 2z_=23,88 suy ra R=2,88 (cm). 3,14
Trả lời: Bán kính hình cầu là R = 2,88cm.
II. BÀI TẬP
16. Cho tam giác đều ABC cạnh 10cm, đường cao AH. Tìm thể tích các hình câu khi quay nửa đường tròn nội tiếp và nửa đường tròn ngoại tiếp tam giác một vòng quanh AH.
17. Chiều cao của một hình trụ gấp 4 lần bán kính đường tròn đáy của nó và có thể tích bằng 42, 46cm. Một hình cầu có bán kính bằng bán kính đường tròn đáy hình trụ thì có thể tích là :
a) 10; b) 14; c) 15; d) 12.
Hãy chọn kết quả đúng trong các kết quả trên.
(Lấy = 3,14 và làm tròn đến cm).
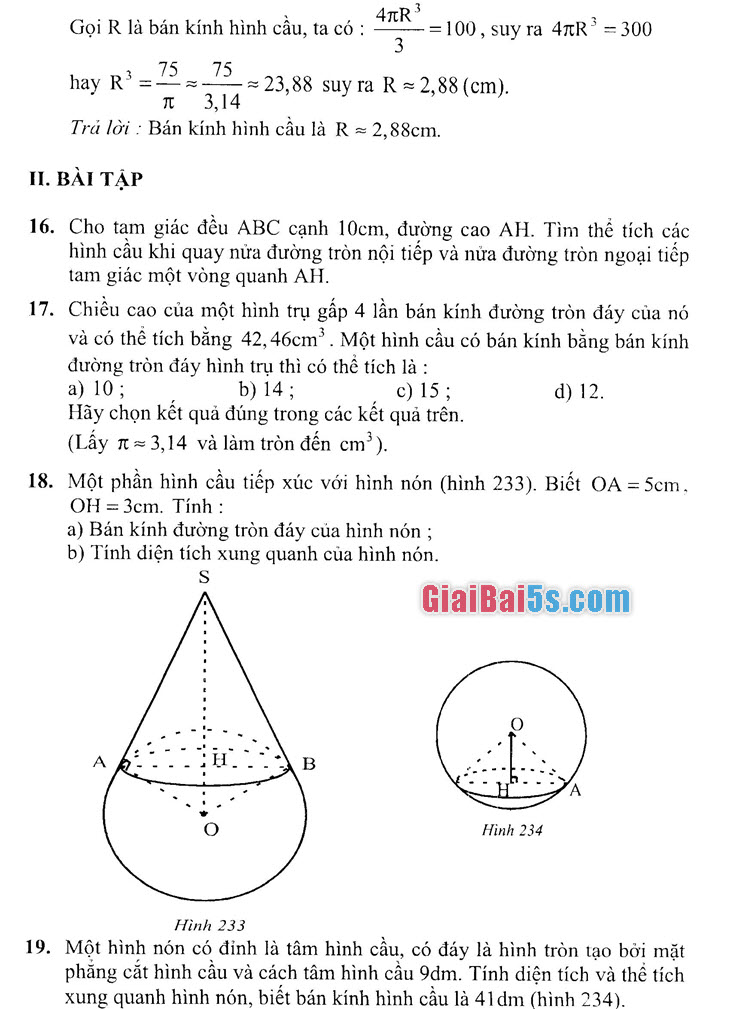
18. Một phần hình cầu tiếp xúc với hình nón (hình 233). Biết OA = 5cm, OH = 3cm. Tính :
a) Bán kính đường tròn đáy của hình nón ;
b) Tính diện tích xung quanh của hình nón.
19. Một hình nón có đỉnh là tấm hình cầu, có đáy là hình tròn tạo bởi mặt phẳng cắt hình cầu và cách tấm hình cầu idm. Tính diện tích và thể tích xung quanh hình nón, biết bán kính hình cầu là 41dm (hình 234).
20. Cho tam giác ABC vuông ở A, đường cao AH. Cho ba nửa đường tròn ngoại tiếp ba tam giác vuông ABH, ACH và ABC lần lượt quay quanh các cạnh AB, AC, BC một vòng, được ba hình cầu.
Chứng minh rằng diện tích mặt cầu nhận BC làm đường kính bằng tổng các diện tích của hai mặt cầu còn lại.
III. HƯỚNG DẪN GIẢI – ĐÁP SỐ
16. AH là đường cao của tam giác đều.
Dễ dàng tính được : AH = ABV3 – 10/3 = 513 (em).
2 2 Gọi O là tâm của tam giác đều thì O là tâm của đường tròn nội tiếp và tâm đường tròn ngoại tiếp AABC.
Vậy OH = 53 (cm) và OA =103 (cm).
OH chính là bán kính hình cầu được tạo ra khi quay nửa đường tròn nội tiếp AABC quanh AH một vòng, ta có OH = 9m.
Thể tích của hình cầu này là :
(513 V 4_53.3V3_5007311 =100,60 (cm’)
1-3″. 3327
OA chính là bán kính hình cầu tạo ra khi quay nửa đường tròn ngoại
_1013 ABC quanh AH một vòng, ta có OA = R =
Thể tích của hình cầu này là :
4 (1073 ľ_ 4 1000.313 _4000731100
–
TT.
=— T. –
33
3
(cm)
Suy ra r
17. Thể tích hình trụ : V = T h = 4tr (vì h = 4r)
V 42,46
<= 3,38 do đó r=1,5 (cm) 41 4.3,14
Thể tích hình cầu là: 4 = 4.3,14,15 = 14 (cm)
Vậy chọn b: 14cm.
18. a) AOAI vuông ở H, ta có :
AH? = (A2-OH= 52 – 32 = 16, suy ra AH = 4 (cm).
b) Tam giác OAS vuông ở A có AH IOS.
Theo hệ thức lượng trong tain giác vuông, ta có :
OAP=OH.OS suy ra OS – OA-5-25
V Ta
OH
3
SA?=$02-0A? – 25 – 25 = 25( 25 – 1 – 25.16 Do đó SA = 3 (cm).
Diện tích xung quanh của hình nón là :
20 8011 S = Turl = tr.HA.SA = 11.4.-= 001–83,73 (cm2)
3 3
19. Đường sinh của hình nón là bán kính của hình cầu nên :
1=OA =R = 41dm
Khoảng cách từ tâm O hình cầu đến tâm đường tròn đáy của hình nón là OH = 9cm. T
am giác AOH vuông ở H, ta có:
HA’ = OA-OH = 41–9° = 1600, suy ra TIA = 40 (dm).
Diện tích xung quanh của hình nón là :
Sxe = .HA.OA = 7.40.41 = 16401 – 5149,6 (cm”). 20. Gọi S, S, S, lần lượt là diện tích các mặt cầu nhận BC, AB, AC làm
đường kính, ta có:
5 = 48 ( M ) : s. -an ( DE ) : 5 =17 (
AB?
A2
BCP
Vậy S, +S, = 4.
– + 47.
AB? + AC2 -= 47.
— -= 47. 4.
4
= 47.
s (vì AB + AC = BC)
Do đó S =S, +S,.
Giải:
Gọi R, là bán kính của mặt cầu thứ nhất, ta có : 4TR =72,35 suy ra R =72,35=72,35 – -5,76
41 4.3.14 do đó R = 2,4 (cm).
Gọi R, là bán kính của mặt cầu thứ hai thì :
R = R1 = 2,4 = 0,8 (cm)
Diện tích mặt cầu thứ hai là :
S = 47R3 = 4.17.0,8° = 2,5611~8,04 (cm2).
Ví dụ 2 :Một hình trụ có bán kính đường tròn đáy là 5cm, chiều cao 6cm. Một hình cầu có thể tích bằng – thể tích hình trụ nói trên. Hãy tính bán kính hình cầu. (Lấy T = 3,14 ).
Giải:
Thể tích hình trụ là : V = h =T.5.6=150 (cm) Vì thể tích hình cầu bằng , thể tích hình trụ nên thể tích hình cầu là :
3
15017.2 = 1001 (cm)
Gọi R là bán kính hình cầu, ta có : 4 =100,
suy ra 4TR = 300
hay R3 = 2z_=23,88 suy ra R=2,88 (cm). 3,14
Trả lời: Bán kính hình cầu là R = 2,88cm.
II. BÀI TẬP
16. Cho tam giác đều ABC cạnh 10cm, đường cao AH. Tìm thể tích các hình câu khi quay nửa đường tròn nội tiếp và nửa đường tròn ngoại tiếp tam giác một vòng quanh AH.
17. Chiều cao của một hình trụ gấp 4 lần bán kính đường tròn đáy của nó và có thể tích bằng 42, 46cm. Một hình cầu có bán kính bằng bán kính đường tròn đáy hình trụ thì có thể tích là :
a) 10; b) 14; c) 15; d) 12.
Hãy chọn kết quả đúng trong các kết quả trên.
(Lấy = 3,14 và làm tròn đến cm).
18. Một phần hình cầu tiếp xúc với hình nón (hình 233). Biết OA = 5cm, OH = 3cm. Tính :
a) Bán kính đường tròn đáy của hình nón ;
b) Tính diện tích xung quanh của hình nón.
19. Một hình nón có đỉnh là tấm hình cầu, có đáy là hình tròn tạo bởi mặt phẳng cắt hình cầu và cách tấm hình cầu idm. Tính diện tích và thể tích xung quanh hình nón, biết bán kính hình cầu là 41dm (hình 234).
20. Cho tam giác ABC vuông ở A, đường cao AH. Cho ba nửa đường tròn ngoại tiếp ba tam giác vuông ABH, ACH và ABC lần lượt quay quanh các cạnh AB, AC, BC một vòng, được ba hình cầu.
Chứng minh rằng diện tích mặt cầu nhận BC làm đường kính bằng tổng các diện tích của hai mặt cầu còn lại.
III. HƯỚNG DẪN GIẢI – ĐÁP SỐ
16. AH là đường cao của tam giác đều.
Dễ dàng tính được : AH = ABV3 – 10/3 = 513 (em).
2 2 Gọi O là tâm của tam giác đều thì O là tâm của đường tròn nội tiếp và tâm đường tròn ngoại tiếp AABC.
Vậy OH = 53 (cm) và OA =103 (cm).
OH chính là bán kính hình cầu được tạo ra khi quay nửa đường tròn nội tiếp AABC quanh AH một vòng, ta có OH = 9m.
Thể tích của hình cầu này là :
(513 V 4_53.3V3_5007311 =100,60 (cm’)
1-3″. 3327
OA chính là bán kính hình cầu tạo ra khi quay nửa đường tròn ngoại
_1013 ABC quanh AH một vòng, ta có OA = R =
Thể tích của hình cầu này là :
4 (1073 ľ_ 4 1000.313 _4000731100
–
TT.
=— T. –
33
3
(cm)
Suy ra r
17. Thể tích hình trụ : V = T h = 4tr (vì h = 4r)
V 42,46
<= 3,38 do đó r=1,5 (cm) 41 4.3,14
Thể tích hình cầu là: 4 = 4.3,14,15 = 14 (cm)
Vậy chọn b: 14cm.
18. a) AOAI vuông ở H, ta có :
AH? = (A2-OH= 52 – 32 = 16, suy ra AH = 4 (cm).
b) Tam giác OAS vuông ở A có AH IOS.
Theo hệ thức lượng trong tain giác vuông, ta có :
OAP=OH.OS suy ra OS – OA-5-25
V Ta
OH
3
SA?=$02-0A? – 25 – 25 = 25( 25 – 1 – 25.16 Do đó SA = 3 (cm).
Diện tích xung quanh của hình nón là :
20 8011 S = Turl = tr.HA.SA = 11.4.-= 001–83,73 (cm2)
3 3
19. Đường sinh của hình nón là bán kính của hình cầu nên :
1=OA =R = 41dm
Khoảng cách từ tâm O hình cầu đến tâm đường tròn đáy của hình nón là OH = 9cm. T
am giác AOH vuông ở H, ta có:
HA’ = OA-OH = 41–9° = 1600, suy ra TIA = 40 (dm).
Diện tích xung quanh của hình nón là :
Sxe = .HA.OA = 7.40.41 = 16401 – 5149,6 (cm”). 20. Gọi S, S, S, lần lượt là diện tích các mặt cầu nhận BC, AB, AC làm
đường kính, ta có:
5 = 48 ( M ) : s. -an ( DE ) : 5 =17 (
AB?
A2
BCP
Vậy S, +S, = 4.
– + 47.
AB? + AC2 -= 47.
— -= 47. 4.
4
= 47.
s (vì AB + AC = BC)
Do đó S =S, +S,.
